
【题目】如图,在Rt△ABC中,∠B=90°,AB=1,BC= ![]() ,以点C为圆心,CB为半径的弧交CA于点D;以点A为圆心,AD为半径的弧交AB于点E.
,以点C为圆心,CB为半径的弧交CA于点D;以点A为圆心,AD为半径的弧交AB于点E. 
(1)求AE的长度;
(2)分别以点A、E为圆心,AB长为半径画弧,两弧交于点F(F与C在AB两侧),连接AF、EF,设EF交弧DE所在的圆于点G,连接AG,试猜想∠EAG的大小,并说明理由.
【答案】
(1)解:在Rt△ABC中,由AB=1,BC= ![]() ,
,
得AC= ![]() =
= ![]() ,
,
∵以点C为圆心,CB为半径的弧交CA于点D;以点A为圆心,AD为半径的弧交AB于点E
∴BC=CD,AE=AD,
∴AE=AC﹣CD= ![]()
(2)解:∠EAG=36°,理由如下:
∵FA=FE=AB=1,AE= ![]() ,
,
∴ ![]() =
= ![]() ,
,
∴△FAE是黄金三角形,
∴∠F=36°,∠AEF=72°,
∵AE=AG,
∴∠EAG=∠F=36°
【解析】(1)根据在Rt△ABC中利用勾股定理求得AC,根据BC=CD,AE=AD求得AE=AC﹣AD即可.(2)根据FA=FE=AB=1,求得AE可得△FAE是黄金三角形可得∠EAG=∠F=36°.
【考点精析】本题主要考查了勾股定理的概念和相似三角形的判定与性质的相关知识点,需要掌握直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2;相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等)的比等于相似比;相似三角形周长的比等于相似比;相似三角形面积的比等于相似比的平方才能正确解答此题.


科目:初中数学 来源: 题型:
【题目】如图,Rt△ABC中,AB⊥BC,AB=6,BC=4,P是△ABC内部的一个动点,且满足∠PAB=∠PBC,则线段CP长的最小值为( )
A.![]()
B.2
C.![]()
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两城市之间开通了动车组高速列车.已知每隔2h有一列速度相同的动车组列车从甲城开往乙城.如图,OA是第一列动车组列车离开甲城的路程s(km)与运行时间t(h)的函数图象,BC是一列从乙城开往甲城的普通快车距甲城的路程s(km)与运行时间t(h)的函数图象.请根据图中的信息,解答下列问题:
(1)从图象看,普通快车发车时间比第一列动车组列车发车时间 1h(填”早”或”晚”),点B的纵坐标600的实际意义是 ;
(2)请直接在图中画出第二列动车组列车离开甲城的路程s(km)与时间t(h)的函数图象;
(3)若普通快车的速度为100km/h,
①求第二列动车组列车出发多长时间后与普通快车相遇?
②请直接写出这列普通快车在行驶途中与迎面而来的相邻两列动车组列车相遇的时间间隔.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知二次函数y=x2+bx+c的图象与x轴交于A,B两点,与y轴交于点P,顶点为C(1,﹣2).
(1)求此函数的关系式;
(2)作点C关于x轴的对称点D,顺次连接A,C,B,D.若在抛物线上存在点E,使直线PE将四边形ACBD分成面积相等的两个四边形,求点E的坐标;
(3)在(2)的条件下,抛物线上是否存在一点F,使得△PEF是以P为直角顶点的直角三角形?若存在,求出点F的坐标及△PEF的面积;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,为了测量某建筑物CD的高度,先在地面上用测角仪自A处测得建筑物顶部的仰角是30°,然后在水平地面上向建筑物前进了100m,此时自B处测得建筑物顶部的仰角是45°.已知测角仪的高度是1.5m,请你计算出该建筑物的高度.(取 ![]() =1.732,结果精确到1m)
=1.732,结果精确到1m)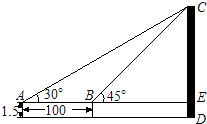
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,等腰梯形MNPQ的上底长为2,腰长为3,一个底角为60°.正方形ABCD的边长为1,它的一边AD在MN上,且顶点A与M重合.现将正方形ABCD在梯形的外面沿边MN、NP、PQ进行翻滚,翻滚到有一个顶点与Q重合即停止滚动.
(1)请在所给的图中,用尺规画出点A在正方形整个翻滚过程中所经过的路线图;
(2)求正方形在整个翻滚过程中点A所经过的路线与梯形MNPQ的三边MN、NP、PQ所围成图形的面积S. 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一只不透明的袋子中装有2个白球和1个红球,这些球除颜色外其余都相同,搅匀后从中任意摸出1个球,记录下颜色后放回袋中并搅匀,再从中任意摸出1个球.请用画树状图的方法列出所有可能的结果,并写出两次摸出的球颜色相同的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,小明在大楼30米高(即PH=30米)的窗口P处进行观测,测得山坡上A处的俯角为15°,山脚B处的俯角为60°,巳知该山坡的坡度i(即tan∠ABC)为1: ![]() ,点P,H,B,C,A在同一个平面上,点H、B、C在同一条直线上,且PH丄HC.
,点P,H,B,C,A在同一个平面上,点H、B、C在同一条直线上,且PH丄HC.
(1)山坡坡角(即∠ABC)的度数等于度;
(2)求A、B两点间的距离(结果精确到0.1米,参考数据: ![]() ≈1.732).
≈1.732).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】公交总站(A点)与B、C两个站点的位置如图所示,已知AC=6km,∠B=30°,∠C=15°,求B站点离公交总站的距离即AB的长(结果保留根号). 
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com