
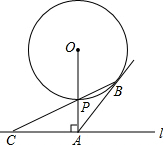
 如图,已知直线l与⊙O相离,OA⊥l于点A,OA=5,OA与⊙O相交于点P,AB与⊙O相切于点B,BP的延长线交直线l于点C.
如图,已知直线l与⊙O相离,OA⊥l于点A,OA=5,OA与⊙O相交于点P,AB与⊙O相切于点B,BP的延长线交直线l于点C.分析 (1)连接OB,根据切线的性质和垂直得出∠OBA=∠OAC=90°,推出∠OBP+∠ABP=90°,∠ACP+∠CPA=90°,求出∠ACP=∠ABC,根据等腰三角形的判定推出即可;
(2)延长AP交⊙O于D,连接BD,设圆半径为r,则OP=OB=r,PA=5-r,根据AB=AC推出52-r2=(2$\sqrt{5}$)2-(5-r)2,求出r.
解答 解:(1)AB=AC,理由如下:
连接OB.如图1,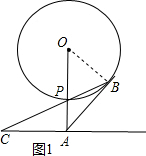
∵AB切⊙O于B,OA⊥AC,
∴∠OBA=∠OAC=90°,
∴∠OBP+∠ABP=90°,∠ACP+∠APC=90°,
∵OP=OB,
∴∠OBP=∠OPB,
∵∠OPB=∠APC,
∴∠ACP=∠ABC,
∴AB=AC;
(2)延长AP交⊙O于D,连接BD,如图2,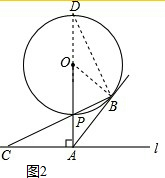
设圆半径为r,则OP=OB=r,PA=5-r,
则AB2=OA2-OB2=52-r2,
AC2=PC2-PA2=(2$\sqrt{5}$)2-(5-r)2,
∴52-r2=(2$\sqrt{5}$)2-(5-r)2,
解得:r=3.
答:⊙O的半径为3.
点评 本题考查了等腰三角形的性质和判定,相似三角形的性质和判定,切线的性质,勾股定理,直线与圆的位置关系等知识点的应用,主要培养学生运用性质进行推理和计算的能力.本题综合性比较强,有一定的难度.


 数学奥赛暑假天天练南京大学出版社系列答案
数学奥赛暑假天天练南京大学出版社系列答案科目:初中数学 来源: 题型:解答题
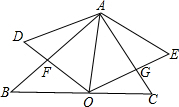 如图,锐角△ABC中,∠BAC=60°,O是BC边上的一点,连接AO,以AO为边向两侧作等边△AOD和等边△AOE,分别与边AB,AC交于点F,G.求证:AF=AG.
如图,锐角△ABC中,∠BAC=60°,O是BC边上的一点,连接AO,以AO为边向两侧作等边△AOD和等边△AOE,分别与边AB,AC交于点F,G.求证:AF=AG.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
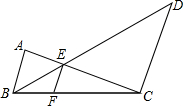 如图,AB∥EF∥DC,AB=20,CD=80,
如图,AB∥EF∥DC,AB=20,CD=80,查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | a>2016 | B. | a<2016 | C. | a>505 | D. | a<505 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com