
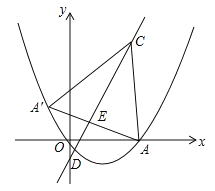
【题目】如图所示,抛物线![]() 经过原点O与点A(6,0)两点,过点A作AC⊥x轴,交直线y=2x﹣2于点C,且直线y=2x﹣2与x轴交于点D.
经过原点O与点A(6,0)两点,过点A作AC⊥x轴,交直线y=2x﹣2于点C,且直线y=2x﹣2与x轴交于点D.
(1)求抛物线的解析式,并求出点C和点D的坐标;
(2)求点A关于直线y=2x﹣2的对称点A′的坐标,并判断点A′是否在抛物线上,并说明理由;
(3)点P(x,y)是抛物线上一动点,过点P作y轴的平行线,交线段CA′于点Q,设线段PQ的长为l,求l与x的函数关系式及l的最大值.
【答案】(1)![]() ,C(6,10),D(1,0);(2)A′(﹣2,4),A′在抛物线上;(3)l=
,C(6,10),D(1,0);(2)A′(﹣2,4),A′在抛物线上;(3)l=![]() ,(﹣2<x≤6),l的最大值为
,(﹣2<x≤6),l的最大值为![]() .
.
【解析】
试题分析:(1)把点O(0,0),A(6,0)代入![]() ,得:
,得:![]() ,解得:
,解得:![]() ,∴抛物线解析式为
,∴抛物线解析式为![]() .
.
当x=6时,y=2×6﹣2=10,当y=0时,2x﹣2=0,解得x=1,∴点C坐标(6,10),点D的坐标(1,0);
(2)过点A′作AF⊥x轴于点F,∵点D(1,0),A(6,0),可得AD=5,在Rt△ACD中,CD=![]() =
=![]() ,∵点A与点A′关于直线y=2x﹣2对称,∴∠AED=90°,∴S△ADC=
,∵点A与点A′关于直线y=2x﹣2对称,∴∠AED=90°,∴S△ADC=![]() ×
×![]() AE=
AE=![]() ×5×10,解得AE=
×5×10,解得AE=![]() ,∴AA′=2AE=
,∴AA′=2AE=![]() ,DE=
,DE=![]() =
=![]() ,∵∠AED=∠AFA′=90°,∠DAE=∠A′AF,∴△ADE∽△AA′F,∴
,∵∠AED=∠AFA′=90°,∠DAE=∠A′AF,∴△ADE∽△AA′F,∴![]() ,解得AF=4,A′F=8,∴OF=8﹣6=2,∴点A′坐标为(﹣2,4),当x=﹣2时,y=
,解得AF=4,A′F=8,∴OF=8﹣6=2,∴点A′坐标为(﹣2,4),当x=﹣2时,y=![]() ,∴A′在抛物线上.
,∴A′在抛物线上.
(3)∵点P在抛物线上,则点P(x,![]() ),设直线A′C的解析式为y=kx+b,∵直线A经过A′(﹣2,4),C(6,10)两点,∴
),设直线A′C的解析式为y=kx+b,∵直线A经过A′(﹣2,4),C(6,10)两点,∴![]() ,解得:
,解得: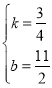 ,∴直线A′C的解析式为
,∴直线A′C的解析式为![]() ,∵点Q在直线A′C上,PQ∥AC,点Q的坐标为(x,
,∵点Q在直线A′C上,PQ∥AC,点Q的坐标为(x,![]() ),∵PQ∥AC,又点Q在点P上方,∴l=(
),∵PQ∥AC,又点Q在点P上方,∴l=(![]() )﹣(
)﹣(![]() )=
)=![]() ,∴l与x的函数关系式为l=
,∴l与x的函数关系式为l=![]() ,(﹣2<x≤6),∵l=
,(﹣2<x≤6),∵l=![]() =
=![]() ,∴当x=
,∴当x=![]() 时,l的最大值为
时,l的最大值为![]() .
.



 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】综合题:探索发现
(1)分解因式:①(1+x)+x(1+x)=()()=()2
②(1+x)+x(1+x) + x(1+x)2=
③(1+x)+x(1+x) + x(1+x)2 + x(1+x)3=
(2)根据(1)的规律,直接写出多项式:(1+x) +x(1+x) + x(1+x)2+…+ x(1+x)2017分解因式的结果:。
(3)变式: ![]() = .
= .
查看答案和解析>>
科目:初中数学 来源: 题型:
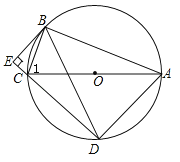
【题目】如图,⊙O是△ABC的外接圆,AC为直径,弦BD=BA,BE⊥DC交DC的延长线于点E,求证:
(1)∠1=∠BAD;
(2)BE是⊙O的切线.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1.2计算3.4分解因式)
(1)( ![]() +1)0﹣(﹣
+1)0﹣(﹣ ![]() )2+2﹣2
)2+2﹣2
(2)(2a﹣3b)(﹣3b﹣2a)
(3)3m2﹣24m+48
(4)x3y﹣4xy.
查看答案和解析>>
科目:初中数学 来源: 题型:
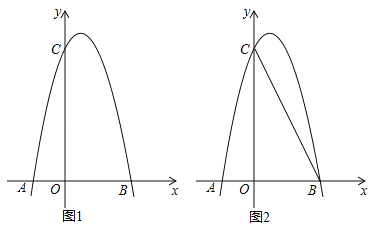
【题目】如图1,对称轴为直线x=![]() 的抛物线经过B(2,0)、C(0,4)两点,抛物线与x轴的另一交点为A.
的抛物线经过B(2,0)、C(0,4)两点,抛物线与x轴的另一交点为A.
(1)求抛物线的解析式;
(2)若点P为第一象限内抛物线上的一点,设四边形COBP的面积为S,求S的最大值;
(3)如图2,若M是线段BC上一动点,在x轴是否存在这样的点Q,使△MQC为等腰三角形且△MQB为直角三角形?若存在,求出点Q的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
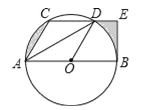
【题目】如图,CD是⊙O的弦,AB是直径,且CD∥AB,连接AC、AD、OD,其中AC=CD,过点B的切线交CD的延长线于E.
(1)求证:DA平分∠CDO;
(2)若AB=12,求图中阴影部分的周长之和(参考数据:π=3.1,![]() =1.4,
=1.4,![]() =1.7).
=1.7).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,把△ABC向上平移4个的那位长度,再向右平移3个单位长度,得到△A′B′C′.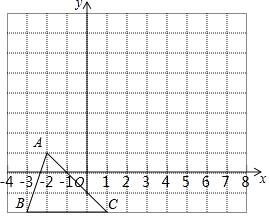
(1)在图中画出△A′B′C′;
(2)连接A′A、C′C,求四边形A′AC′C的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】按一定规律排列的一列数:21 , 22 , 23 , 25 , 28 , 213 , …,若x、y、z表示这列数中的连续三个数,猜想x、y、z满足的关系式是 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com