
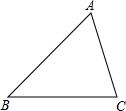
 按下列要求画图,并解答问题:
按下列要求画图,并解答问题:分析 (1)先作BC的垂直平分线得到BC的中点D,然后作射线AD;
(2)利用基本作图(过一点作已知直线的垂线)作出BE和CF;
(3)根据平行线的性质易得BE∥CF,然后证明△BED≌△CFD得到BE=CF.
解答 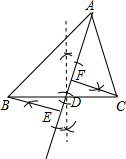 解:(1)AD为所作,如图:
解:(1)AD为所作,如图:
(2)BE、CF为所作,如图:
(3)BE=CF,BE∥CF.理由如下:
∵BE⊥AD,CF⊥AD,
∴BE∥CF,∠BED=∠CFD=90°,
∵D为BC的中点,
∴BD=CD,
在△BED和△CFD中,
$\left\{\begin{array}{l}{∠BED=∠CFD}\\{∠BDE=∠CDF}\\{BD=CD}\end{array}\right.$,
∴△BED≌△CFD,
∴BE=CF.
故答案为:相等,平行.
点评 本题考查了基本作图:掌握5个基本作图(作一条线段等于已知线段;作一个角等于已知角;作已知线段的垂直平分线;作已知角的角平分线;过一点作已知直线的垂线).也考查了三角形全等的判定与性质.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
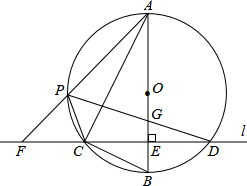 如图,△ABC是⊙O的内接三角形,且AB是⊙O的直径,AC=2BC,过点C作AB的垂线l交于AB于点E,交⊙O于点D,设点P是$\widehat{AB}$上异于A,C的一个动点,AP的连线交l于点F,连接PC与PD;
如图,△ABC是⊙O的内接三角形,且AB是⊙O的直径,AC=2BC,过点C作AB的垂线l交于AB于点E,交⊙O于点D,设点P是$\widehat{AB}$上异于A,C的一个动点,AP的连线交l于点F,连接PC与PD;查看答案和解析>>
科目:初中数学 来源: 题型:填空题
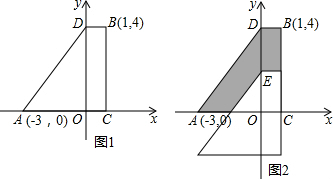
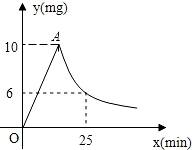 由于天气炎热,某校根据《学校卫生工作条例》,为预防“蚊虫叮咬”,对教室进行“薰药消毒”.已知药物在燃烧机释放过程中,室内空气中每立方米含药量y(毫克)与燃烧时间x(分钟)之间的关系如图所示(即图中线段OA和双曲线在A点及其右侧的部分),当空气中每立方米的含药量低于2毫克时,对人体无毒害作用,那么从消毒开始,至少在72分钟内,师生不能呆在教室.
由于天气炎热,某校根据《学校卫生工作条例》,为预防“蚊虫叮咬”,对教室进行“薰药消毒”.已知药物在燃烧机释放过程中,室内空气中每立方米含药量y(毫克)与燃烧时间x(分钟)之间的关系如图所示(即图中线段OA和双曲线在A点及其右侧的部分),当空气中每立方米的含药量低于2毫克时,对人体无毒害作用,那么从消毒开始,至少在72分钟内,师生不能呆在教室.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 为了了解全班同学的视力情况,采用全面调查 | |
| B. | 为调查乘坐飞机的旅客是否携带了违禁物品,采用抽样调查 | |
| C. | 为了解某一种节能灯的使用寿命,采用全面调查 | |
| D. | 为了解某鱼塘里鱼的生长情况,采用全面调查 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com