
【题目】如图,已知顶点为(﹣3,﹣6)的抛物线y=ax2+bx+c经过点(﹣1,﹣4),则下列结论中错误的是( )
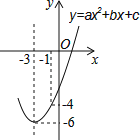
A. b2>4ac
B. ax2+bx+c≥﹣6
C. 关于x的一元二次方程ax2+bx+c=﹣4的两根分别为﹣5和﹣1
D. 若点(﹣2,m),(﹣5,n)在抛物线上,则m>n
【答案】D
【解析】
根据抛物线与x轴有两个交点判断出A选项结论正确,二次函数的顶点的意义判断出B选项结论正确;根据顶点坐标求出抛物线的对称轴,然后根据二次函数的对称性求解即可判断出C选项结论正确;根据两点与对称轴的距离以及二次函数的增减性判断出D选项结论错误.
A、∵抛物线与x轴有两个交点,
∴b2﹣4ac>0,
∴b2>4ac,结论正确,故本选项错误;
B、∵抛物线顶点坐标为(﹣3,﹣6),开口向上,
∴ax2+bx+c≥﹣6,结论正确,故本选项错误;
C、∵抛物线y=ax2+bx+c经过点(﹣1,﹣4),
∴关于x的一元二次方程ax2+bx+c=﹣4的一个根为﹣1,
∵抛物线对称轴为直线x=﹣3,
∴另一个根为2×(﹣3)﹣(﹣1)=﹣6+1=﹣5,结论正确,故本选项错误;
D、∵﹣2﹣(﹣3)=1,(﹣3)﹣(﹣5)=2,
∴点(﹣5,n)到对称轴的距离比点(﹣2,m)到对称轴的距离大,
∴m<n,本选项结论错误,故本选项正确.
故选:D.


 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案科目:初中数学 来源: 题型:
【题目】亚健康是时下社会热门话题,进行体育锻炼是远离亚健康的一种重要方式,为了解某市初中学生每天进行体育锻炼的时间情况,随机抽样调查了100名初中学生,根据调查结果得到如图所示的统计图表.
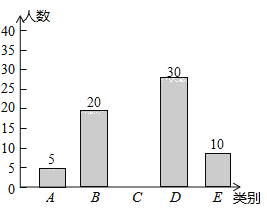
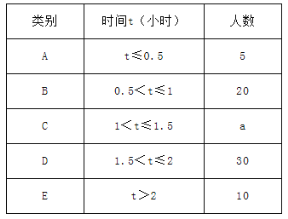
请根据图表信息解答下列问题:
(1)a=_____;
(2)补全条形统计图;
(3)小王说:“我每天的锻炼时间是调查所得数据的中位数”,问小王每天进行体育锻炼的时间在什么范围内?
(4)据了解该市大约有30万名初中学生,请估计该市初中学生每天进行体育锻炼时间在1小时以上的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场用2500元购进A、B两种新型节能台灯共50盏,这两种台灯的进价、标价如下表所示.
类型 价格 | A型 | B型 |
进价(元/盏) | 40 | 65 |
标价(元/盏) | 60 | 100 |
(1)这两种台灯各购进多少盏?
(2)在每种台灯销售利润不变的情况下,若该商场计划销售这批台灯的总利润至少为1400元,问至少需购进B种台灯多少盏?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某水果批发商经营甲、乙两种水果,根据以往经验和市场行情,预计夏季某一段时间内,甲种水果的销售利润![]() (万元)与进货量x(吨)近似满足函数关系
(万元)与进货量x(吨)近似满足函数关系![]() ,乙种水果的销售利润
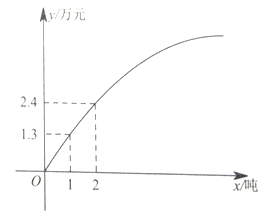
,乙种水果的销售利润![]() (万元)与进货量x(吨)之间的函数关系如图所示.
(万元)与进货量x(吨)之间的函数关系如图所示.
(1)求![]() (万元)与x(吨)之间的函数关系式;
(万元)与x(吨)之间的函数关系式;
(2)如果该批发商准备进甲、乙两种水果共10吨,设乙种水果的进货量为t吨,请你求出这两种水果所获得的销售利润总和W(万元)与t(吨)之间的函数关系式.并求出这两种水果各进多少吨时获得的销售利润总和最大,最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学校植物园沿路护栏的纹饰部分设计成若干个全等菱形图案,每增加一个菱形图案,纹饰长度就增加dcm,如图所示,已知每个菱形图案的边长为10![]() cm,其中一个内角为60°.
cm,其中一个内角为60°.
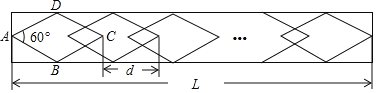
(1)求一个菱形图案水平方向的对角线长;
(2)若d=26,纹饰的长度L能否是6010cm?若能,求出菱形个数;若不能,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
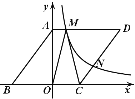
【题目】如图,菱形ABCD的顶点A在y轴正半轴上,边BC在x轴上,且BC=5,sin∠ABC=![]() ,反比例函数
,反比例函数![]() (x>0)的图象分别与AD,CD交于点M、点N,点N的坐标是(3,n),连接OM,MC.
(x>0)的图象分别与AD,CD交于点M、点N,点N的坐标是(3,n),连接OM,MC.
(1)求反比例函数的解析式;
(2)求证:△OMC是等腰三角形.
查看答案和解析>>
科目:初中数学 来源: 题型:
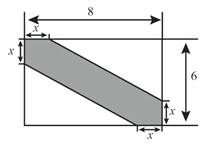
【题目】某景区内有一块矩形油菜花田地(数据如图示,单位:m.)现在其中修建一条观花道(图中阴影部分)供游人赏花.设改造后剩余油菜花地所占面积为ym2.
(1)求y与x的函数表达式;
(2)若改造后观花道的面积为13m2,求x的值;
(3)若要求 0.5≤ x ≤1,求改造后剩余油菜花地所占面积的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
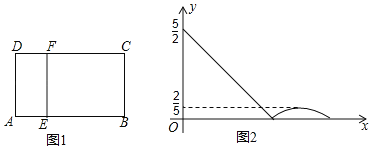
【题目】如图1,在矩形ABCD中,动点E从A出发,沿AB→BC方向运动,当点E到达点C时停止运动,过点E做FE⊥AE,交CD于F点,设点E运动路程为x,FC=y,如图2所表示的是y与x的函数关系的大致图象,当点E在BC上运动时,FC的最大长度是![]() ,则矩形ABCD的面积是( )
,则矩形ABCD的面积是( )
A. ![]() B. 5C. 6D.
B. 5C. 6D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商品的进价为每件50元.当售价为每件70元时,每星期可卖出300件,现需降价处理,且经市场调查:每降价1元,每星期可多卖出20件.在确保盈利的前提下,解答下列问题:
(1)若设每件降价x元、每星期售出商品的利润为y元,请写出y与x的函数关系式,并求出自变量x的取值范围;
(2)当降价多少元时,每星期的利润最大?最大利润是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com