
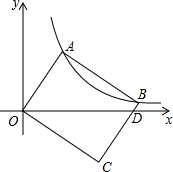
 如图,在直角坐标系中,矩形OABC的顶点A、B在双曲线y=
如图,在直角坐标系中,矩形OABC的顶点A、B在双曲线y=| k |
| x |
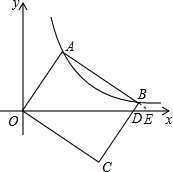 解:∵A在双曲线上,
解:∵A在双曲线上,| 2 |
| x |
| 1 |
| 2 |
| 5 |
| 2 |
| 1 |
| 2 |
| 5 |
| 2 |
|
|
|
| 1 |
| 2 |
| 1 |
| 2 |
| 15 |
| 2 |
| 15 |
| 2 |
| 15 |
| 2 |
| 15 |
| 4 |
| 15 |
| 4 |
| 1 |
| 2 |
| 5 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 15 |
| 4 |
| 1 |
| 2 |
| 5 |
| 16 |
| 75 |
| 16 |


 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案 初中学业考试导与练系列答案
初中学业考试导与练系列答案科目:初中数学 来源: 题型:
| 10 |
| 3 |
| • |
| 1 |
| • |
| 5 |
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,四边形ABCD中,过点D作DE⊥AB,作DF⊥BC,垂足分别为点E、F,∠EDF=60°,若BE=14,BF=2,求平行四边形ABCD的周长和面积.
如图,四边形ABCD中,过点D作DE⊥AB,作DF⊥BC,垂足分别为点E、F,∠EDF=60°,若BE=14,BF=2,求平行四边形ABCD的周长和面积.查看答案和解析>>
科目:初中数学 来源: 题型:
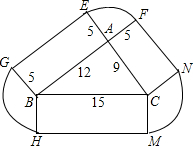 如图所示,一个房屋地基呈三角形状.三角形的边长分别为9米、12米、15米,花园由距地基边界5米之内的土地构成,问房屋连同花园共占地多少平方米?(精确到1平方米)
如图所示,一个房屋地基呈三角形状.三角形的边长分别为9米、12米、15米,花园由距地基边界5米之内的土地构成,问房屋连同花园共占地多少平方米?(精确到1平方米)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com