
【题目】已知抛物线y=2x2+bx+c经过点A(2,-1) .
(1)若抛物线的对称轴为x=1,求b,c的值;
(2)求证:抛物线与x轴有两个不同的交点;
(3)设抛物线顶点为P,若O、A、P三点共线(O为坐标原点),求b的值.
【答案】(1)b=-4 ,c=-1;(2)证明见解析;(3)b=-8或b=-9.
【解析】分析:(1)根据对称轴为x=1,可得![]() ,可求出b的值,再把A(2,-1)代入到y=2x2+bx+c求出c的值;
,可求出b的值,再把A(2,-1)代入到y=2x2+bx+c求出c的值;
(2)求出b2-4ac的值,然后可判断出二次函数图像与x轴的交点个数;
(3)先求出直线OA的解析式,把把A(2,-1)代入到y=2x2+bx+c求出b,c之间的关系,根据顶点坐标![]() 表示出点P的坐标,代入直线OA的解析式,求出b的值.
表示出点P的坐标,代入直线OA的解析式,求出b的值.
详解:(1)∵抛物线的对称轴为x=1,
∴-![]() =-=1,∴b=-4
=-=1,∴b=-4
将点A(2,-1)代入y=2x2-4x+c中,解得c=-1;
(2)∵b2-4ac=b2-8c,将(2,-1)代入y=2x2+bx+c,得c=-2b-9,
即b2-4ac=b2-8(-2b-9)=(b+8)2+8>0,
∴方程2x2+bx+c=0有两个不相等的实数根,
∴抛物线与x轴有两个不同的交点
(3)抛物线顶点坐标为(-,![]() ),
),
直线OA关系式为y=-x,将顶点坐标代入直线OA,
得方程b2+17b+72=0
求得b=-8或b=-9.


科目:初中数学 来源: 题型:
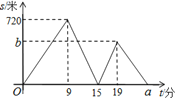
【题目】小明、小华从学校出发到青少年宫参加书法比赛,小明步行一段时间后,小华骑自行车沿相同路线行进,两人均匀速前行.他们的路程差s (米)与小明出发时间t (分)之间的函数关系如图所示.下列说法:
①小华先到达青少年宫;②小华的速度是小明速度的2.5倍;③a=24;④b=480.其中正确的是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
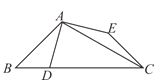
【题目】如图,△ABC中,∠ABC=45°,∠BCA=30°,点D在BC上,点E在△ABC外,且AD=AE=CE,AD⊥AE,则![]() 的值为____________.
的值为____________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在课题学习中,老师要求用长为12厘米,宽为8厘米的长方形纸片制作一个无盖的长方体纸盒.三位同学分别以下列方式在长方形纸片上截去两角(图中阴影部分),然后沿虚线折成一个无盖的长方体纸盒.
甲:如图1,盒子底面的四边形ABCD是正方形;
乙:如图2,盒子底面的四边形ABCD是正方形;
丙:如图3,盒子底面的四边形ABCD是长方形,AB=2AD.
将这三位同学所折成的无盖长方体的容积按从大到小的顺序排列,正确的是

A.甲>乙>丙B.甲>丙>乙C.丙>甲>乙D.丙>乙>甲
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在菱形ABCD中,G是BD上一点,连接CG并延长交BA的延长线于点F,交AD于点E.

(1)求证:△ADG≌△CDG.
(2)若![]() =
=![]() ,EG=4,求AG的长.
,EG=4,求AG的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=x2+bx+c与x轴交于A(﹣1,0),B(3,0)两点,顶点M关于x轴的对称点是M′.
(1)求抛物线的解析式;
(2)若直线AM′与此抛物线的另一个交点为C,求△CAB的面积;
(3)是否存在过A,B两点的抛物线,其顶点P关于x轴的对称点为Q,使得四边形APBQ为正方形?若存在,求出此抛物线的解析式;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线AB,CD相交于点O,∠BOE=90°,OF平分∠AOD,∠COE=20°.
(1)求∠BOD与∠DOF的度数.
(2)写出∠COE的所有余角.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将正方形ABCD折叠,使顶点A与CD边上的一点H重合(H不与端点C,D重合),折痕交AD于点E,交BC于点F,边AB折叠后与边BC交于点G,如果正方形ABCD的边长为1,则△CHG的周长为__________

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com