
【题目】如图,直线AB,CD相交于点O,∠BOE=90°,OF平分∠AOD,∠COE=20°.
(1)求∠BOD与∠DOF的度数.
(2)写出∠COE的所有余角.

【答案】(1)∠BOD==70°,∠DOF=55°;(2)∠COA,∠BOD.
【解析】
(1)根据邻补角的定义得到∠AOE=180°-∠BOE=180°-90°=90°,求得∠AOD=180°-∠COA=180°-70°=110°,根据角平分线的定义即可得到结论;
(2)根据余角的性质即可得到结论.
(1)∵∠BOE=90°,
∴∠AOE=180°﹣∠BOE=180°﹣90°=90°,
∵∠COE=20°,
∴∠COA=90°﹣∠COE=90°﹣20°=70°,
∴∠BOD=∠COA=70°,
∴∠AOD=180°﹣∠COA=180°﹣70°=110°,
又∵OF平分∠AOD,
∴∠DOF=![]() ∠AOD=
∠AOD=![]() 110°=55°;
110°=55°;
(2)∵∠AOE=90°,
∴∠AOC+∠COE=90°,
∵∠BOD=∠AOC,
∴∠BOD+∠COE=90°,
∴∠COE的余角有:∠COA,∠BOD.


科目:初中数学 来源: 题型:
【题目】已知△ABC是等边三角形,D是BC边上的一个动点(点D不与B,C重合)△ADF是以AD为边的等边三角形,过点F作BC的平行线交射线AC于点E,连接BF.

(1)如图1,求证:△AFB≌△ADC;
(2)请判断图1中四边形BCEF的形状,并说明理由;
(3)若D点在BC 边的延长线上,如图2,其它条件不变,请问(2)中结论还成立吗?如果成立,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=2x2+bx+c经过点A(2,-1) .
(1)若抛物线的对称轴为x=1,求b,c的值;
(2)求证:抛物线与x轴有两个不同的交点;
(3)设抛物线顶点为P,若O、A、P三点共线(O为坐标原点),求b的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,ABCD的对角线AC,BD相交于点O.E,F是AC上的两点,并且AE=CF,连接DE,BF.
(1)求证:△DOE≌△BOF;
(2)若BD=EF,连接DE,BF.判断四边形EBFD的形状,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(一)如下图①:把三个正方形摆成一定的形状。
问题(1):
若图中的三角形△DEF为直角三角形,P的面积为9,Q的面积为15,则M的面积为( ).
问题(2):
若P的面积为36cm2,Q的面积为64cm2,同时M的面积为100cm2,则△DEF为( )三角形.
(二)图形变化:
如图②,分别以直角△ABC的三边为直径向三角形外作三个半圆,你能找出这三个半圆的面积之间有什么关系吗?请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知a、b、c在数轴上的位置如图所示,所对应的点分别为A、B、C,
![]()
(1)在数轴上表示2的点与表示5的点之间的距离为 ;
在数轴上表示﹣1的点与表示3的点之间的距离为 ;在数轴上表示﹣3的点与表示﹣5的点之间的距离为 ;由此可得点A、B之间的距离为 ,点B、C之间的距离为 ,点A、C之间的距离为 ;
(2)化简:﹣|a+b|+|c﹣b|﹣|b﹣a|;
(3)若c2=4,﹣b的倒数是它本身,a的绝对值的相反数是﹣2,求﹣a+2b﹣c﹣(a﹣4c﹣b)的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2017年12月3日至5日,第四届世界互联网大会在浙江省乌镇举行.会议期间,某公司的无人超市,让人们感受到互联网新零售带来的全新体验.小张购买了钥匙扣和毛绒玩具两种商品共15件,离开超市后,收到短信显示,购买钥匙扣支付240元,购买毛绒玩具支付180元.已知毛绒玩具的单价是钥匙扣单价的1.5倍,那么钥匙扣和毛绒玩具的单价各是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某数学兴趣小组同学进行测量大树CD高度的综合实践活动,如右图,在点A处测得直立于地面的大树顶端C的仰角为45°,然后沿在同一剖面的斜坡AB行走13米至坡顶B处,然后再沿水平方向行走6米至大树脚底点D处,斜面AB的坡度(或坡比)i=1∶2.4,那么大树CD的高度约为多少?( )

A. 18米 B. 13米 C. 12米 D. 5米
查看答案和解析>>
科目:初中数学 来源: 题型:
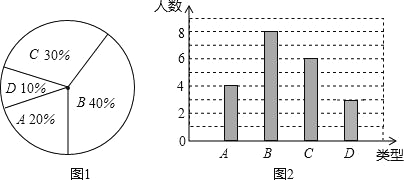
【题目】某校260名学生参加植树活动,要求每人植4~7棵,活动结束后随机抽查了若干名学生每人的植树量,并分为四种类型, A:4棵;B:5棵;C:6棵;D:7棵,将各类的人数绘制成扇形图(如图1)和条形图(如图2),请回答下列问题:
(1)在这次调查中D类型有多少名学生?
(2)写出被调查学生每人植树量的众数、中位数;
(3)求被调查学生每人植树量的平均数,并估计这260名学生共植树多少棵?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com