
ЁОЬтФПЁП(вЛ)ШчЯТЭМЂйЃКАбШ§Иіе§ЗНаЮАкГЩвЛЖЈЕФаЮзДЁЃ
ЮЪЬтЃЈ1ЃЉЃК
ШєЭМжаЕФШ§НЧаЮЁїDEFЮЊжБНЧШ§НЧаЮЃЌPЕФУцЛ§ЮЊ9ЃЌQЕФУцЛ§ЮЊ15ЃЌдђMЕФУцЛ§ЮЊЃЈ ЃЉЃЎ
ЮЪЬтЃЈ2ЃЉЃК
ШєPЕФУцЛ§ЮЊ36cm2ЃЌQЕФУцЛ§ЮЊ64cm2ЃЌЭЌЪБMЕФУцЛ§ЮЊ100cm2ЃЌдђЁїDEFЮЊЃЈ ЃЉШ§НЧаЮЃЎ
ЃЈЖўЃЉЭМаЮБфЛЏЃК
ШчЭМЂкЃЌЗжБ№вджБНЧЁїABCЕФШ§БпЮЊжБОЖЯђШ§НЧаЮЭтзїШ§ИіАыдВЃЌФуФмевГіетШ§ИіАыдВЕФУцЛ§жЎМфгаЪВУДЙиЯЕТ№ЃПЧыЫЕУїРэгЩЃЎ

 злКЯздВтЯЕСаД№АИ
злКЯздВтЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌЖўДЮКЏЪ§ЕФЭМЯѓгыxжсНЛгкAЃЈЉ3ЃЌ0ЃЉКЭBЃЈ1ЃЌ0ЃЉСНЕуЃЌНЛyжсгкЕуCЃЈ0ЃЌ3ЃЉЃЌЕуCЁЂDЪЧЖўДЮКЏЪ§ЭМЯѓЩЯЕФвЛЖдЖдГЦЕуЃЌвЛДЮКЏЪ§ЕФЭМЯѓЙ§ЕуBЁЂDЃЎ

ЃЈ1ЃЉЧѓЖўДЮКЏЪ§ЕФНтЮіЪНЃЛ
ЃЈ2ЃЉИљОнЭМЯѓжБНгаДГіЪЙвЛДЮКЏЪ§жЕДѓгкЖўДЮКЏЪ§жЕЕФxЕФШЁжЕЗЖЮЇЃЛ
ЃЈ3ЃЉШєжБЯпгыyжсЕФНЛЕуЮЊEЃЌСЌНсADЁЂAEЃЌЧѓЁїADEЕФУцЛ§ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкСтаЮABCDжаЃЌGЪЧBDЩЯвЛЕуЃЌСЌНгCGВЂбгГЄНЛBAЕФбгГЄЯпгкЕуFЃЌНЛADгкЕуEЃЎ

ЃЈ1ЃЉЧѓжЄЃКЁїADGЁеЁїCDGЃЎ
ЃЈ2ЃЉШє![]() ЃН
ЃН![]() ЃЌEGЃН4ЃЌЧѓAGЕФГЄЃЎ
ЃЌEGЃН4ЃЌЧѓAGЕФГЄЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌХзЮяЯпy=x2+bx+cгыxжсНЛгкAЃЈЉ1ЃЌ0ЃЉЃЌBЃЈ3ЃЌ0ЃЉСНЕуЃЌЖЅЕуMЙигкxжсЕФЖдГЦЕуЪЧMЁфЃЎ
ЃЈ1ЃЉЧѓХзЮяЯпЕФНтЮіЪНЃЛ
ЃЈ2ЃЉШєжБЯпAMЁфгыДЫХзЮяЯпЕФСэвЛИіНЛЕуЮЊCЃЌЧѓЁїCABЕФУцЛ§ЃЛ
ЃЈ3ЃЉЪЧЗёДцдкЙ§AЃЌBСНЕуЕФХзЮяЯпЃЌЦфЖЅЕуPЙигкxжсЕФЖдГЦЕуЮЊQЃЌЪЙЕУЫФБпаЮAPBQЮЊе§ЗНаЮЃПШєДцдкЃЌЧѓГіДЫХзЮяЯпЕФНтЮіЪНЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЃЈБОаЁЬтТњЗж10ЗжЃЉ
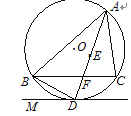
ШчЭМЃЌЕуEЪЧЁїABCЕФФкаФЃЌAEЕФбгГЄЯпНЛBCгкЕуFЃЌНЛЁїABCЕФЭтНгдВЁбOгкЕуDЃЛСЌНгBDЃЌЙ§ЕуDзїжБЯпDMЃЌЪЙЁЯBDMЃНЁЯDACЃЎ
ЃЈ1ЃЉЧѓжЄЃКжБЯпDMЪЧЁбOЕФЧаЯпЃЛ
ЃЈ2ЃЉЧѓжЄЃКDE2ЃНDFЁЄDAЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌжБЯпABЃЌCDЯрНЛгкЕуOЃЌЁЯBOEЃН90ЁуЃЌOFЦНЗжЁЯAODЃЌЁЯCOEЃН20ЁуЃЎ
ЃЈ1ЃЉЧѓЁЯBODгыЁЯDOFЕФЖШЪ§ЃЎ
ЃЈ2ЃЉаДГіЁЯCOEЕФЫљгагрНЧЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПИажЊгыЬюПе:ШчЭМЂйЃЌжБЯп![]() ЃЌЧѓжЄ:
ЃЌЧѓжЄ:![]() .
.

дФЖСЯТУцЕФНтД№Й§ГЬЃЌВЂЬюЩЯЪЪЕБЕФРэгЩЃЌ
Нт:Й§Еу![]() зїжБЯп
зїжБЯп![]() ,
,
![]() ЃЈ ЃЉ
ЃЈ ЃЉ
![]() (вбжЊ)ЃЌ
(вбжЊ)ЃЌ![]() ,
,
![]() ЃЈ ЃЉ
ЃЈ ЃЉ
![]() ЃЈ ЃЉ
ЃЈ ЃЉ
![]() ,
,
![]() ЃЈ ЃЉ
ЃЈ ЃЉ
гІгУгыЭиеЙ:ШчЭМЂкЃЌжБЯп![]() ЃЌШє
ЃЌШє![]() .
.

дђ![]() ЖШ
ЖШ
ЗНЗЈгыЪЕМљ:ШчЭМЂлЃЌжБЯп![]() ЃЌШє
ЃЌШє![]() ,дђ
,дђ![]() ЖШ.
ЖШ.

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЮвЪаФГжабЇОйАьЁАЭјТчАВШЋжЊЪЖД№ЬтОКШќЁБЃЌГѕЁЂИпжаВПИљОнГѕШќГЩМЈИїбЁГі5УћбЁЪжзщГЩГѕжаДњБэЖгКЭИпжаДњБэЖгВЮМгбЇаЃОіШќЃЌСНИіЖгИїбЁГіЕФ5УћбЁЪжЕФОіШќГЩМЈШчЭМЫљЪОЃЎ
ЦНОљЗжЃЈЗжЃЉ | жаЮЛЪ§ЃЈЗжЃЉ | жкЪ§ЃЈЗжЃЉ | ЗНВюЃЈЗж2ЃЉ | |
ГѕжаВП | a | 85 | b | sГѕжа2 |
ИпжаВП | 85 | c | 100 | 160 |
ЃЈ1ЃЉИљОнЭМЪОМЦЫуГіaЁЂbЁЂcЕФжЕЃЛ
ЃЈ2ЃЉНсКЯСНЖгГЩМЈЕФЦНОљЪ§КЭжаЮЛЪ§НјааЗжЮіЃЌФФИіЖгЕФОіШќГЩМЈНЯКУЃП
ЃЈ3ЃЉМЦЫуГѕжаДњБэЖгОіШќГЩМЈЕФЗНВюsГѕжа2ЃЌВЂХаЖЯФФвЛИіДњБэЖгбЁЪжГЩМЈНЯЮЊЮШЖЈЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПГѕвЛЃЈ1ЃЉАреыЖдЁАФузюЯВАЎЕФПЮЭтЛюЖЏЯюФПЁБЖдШЋАрбЇЩњНјааЕїВщЃЈУПУћбЇЩњЗжБ№бЁвЛИіЛюЖЏЯюФПЃЉЃЌВЂИљОнЕїВщНсЙћСаГіЭГМЦБэЃЌЛцжЦГЩЩШаЮЭГМЦЭМЃЎ

ИљОнвдЩЯаХЯЂНтОіЯТСаЮЪЬтЃК
ЃЈ1ЃЉ![]() ЃЌ
ЃЌ![]() ЃЛ
ЃЛ
ЃЈ2ЃЉЩШаЮЭГМЦЭМжаЛњЦїШЫЯюФПЫљЖдгІЩШаЮЕФдВаФНЧЖШЪ§ЮЊ ![]() ЃЛ
ЃЛ
ЃЈ3ЃЉДгбЁКНФЃЯюФПЕФ![]() УћбЇЩњжаЫцЛњбЁШЁ
УћбЇЩњжаЫцЛњбЁШЁ![]() УћбЇЩњВЮМгбЇаЃКНФЃаЫШЄаЁзщбЕСЗЃЌЧыгУСаОйЗЈЃЈЛЪїзДЭМЛђСаБэЃЉЧѓЫљбЁШЁЕФ
УћбЇЩњВЮМгбЇаЃКНФЃаЫШЄаЁзщбЕСЗЃЌЧыгУСаОйЗЈЃЈЛЪїзДЭМЛђСаБэЃЉЧѓЫљбЁШЁЕФ![]() УћбЇЩњжаЧЁКУга
УћбЇЩњжаЧЁКУга![]() УћФаЩњЁЂ
УћФаЩњЁЂ![]() УћХЎЩњЕФИХТЪЃЎ
УћХЎЩњЕФИХТЪЃЎ
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com