
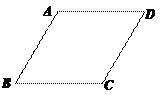
【题目】如图,在菱形ABCD中,G是BD上一点,连接CG并延长交BA的延长线于点F,交AD于点E.

(1)求证:△ADG≌△CDG.
(2)若![]() =
=![]() ,EG=4,求AG的长.
,EG=4,求AG的长.
【答案】(1)证明见解析;(2)AG=6 .
【解析】分析:(1)首先根据菱形的性质得到∠ADG=∠CDG,AD=BC,然后根据“SAS”推出△ADG≌△CDG;
(2)先证明△FAE∽△FBC,可得![]() ,再证明△DGE∽△BGC,求出CG的长,从而可求出AG的长.
,再证明△DGE∽△BGC,求出CG的长,从而可求出AG的长.
详解:(1)∵四边形ABCD是菱形,
∴AB=BC,AD=BC,
又∵BD=BD,
∴△ABD≌△CBD,
∴∠ADB=∠CDB,
又∵AD=CD,DG=DG,
∴△ADG≌△CDG.
(2)∵△ADG≌△CDG,
∴AG=GC,
∵四边形ABCD是菱形,
∴AD∥BC,AD=BC,
∴△FAE∽△FBC,
∴![]() =
=![]() ,
,
∵![]() =,
=,
∴![]() =,
=,
∴![]() =,
=,
∴![]() =.
=.
∵AD∥BC,
∴∠GDE=∠GBC,∠GED=∠GCB,又∠DGE=∠BGC,
∴△DGE∽△BGC,
∴![]() =
=![]() =,
=,
∵EG=4,
∴CG=6,
∴AG=6 .


 互动课堂系列答案
互动课堂系列答案 激活思维智能训练课时导学练系列答案
激活思维智能训练课时导学练系列答案科目:初中数学 来源: 题型:
【题目】某中学九(1)班为了了解全班学生喜欢球类活动的情况,采取全面调查的方法,从足球、乒乓球、篮球、排球等四个方面调查了全班学生的兴趣爱好,根据调查的结果组建了4个兴趣小组,并绘制成如图所示的两幅不完整的统计图(如图①,②,要求每位学生只能选择一种自己喜欢的球类),请你根据图中提供的信息解答下列问题:

(1)九(1)班的学生人数为40,并把条形统计图补充完整;
(2)扇形统计图中m=10,n=20,表示“足球”的扇形的圆心角是72度;
(3)排球兴趣小组4名学生中有3男1女,现在打算从中随机选出2名学生参加学校的排球队,请用列表或画树状图的方法求选出的2名学生恰好是1男1女的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,数轴上A点表示的数是﹣2,B点表示的数是5,C点表示的数是10.
![]()
(1)若要使A、C两点所表示的数是一对相反数,则“原点”表示的数是: .
(2)若此时恰有一只老鼠在B点,一只小猫在C点,老鼠发现小猫后立即以每秒一个单位的速度向点A方向逃跑,小猫随即以每秒两个单位的速度追击.
①在小猫未抓住老鼠前,用时间t(秒)的代数式表示老鼠和小猫在移动过程中分别与点A之间的距离;
②小猫逮住老鼠时的“位置”恰好在 ,求时间t.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,∠BAD的平分线交BC于点E,∠ABC的平分线交AD于点F,若BF=12,AB=10,则AE的长为( )

A. 13B. 14C. 15D. 16
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一艘救生船在码头A接到小岛C处一艘渔船的求救信号,立即出发,沿北偏东67°方向航行10海里到达小岛C处,将人员撤离到位于码头A正东方向的码头B,测得小岛C位于码头B的北偏西53°方向,求码头A与码头B的距离.【参考数据:sin23°≈0.39,cos23°≈0.92,tan23°≈0.42,sin37°≈0.60,cos37°≈0.80,tan37°≈0.75】

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=2x2+bx+c经过点A(2,-1) .
(1)若抛物线的对称轴为x=1,求b,c的值;
(2)求证:抛物线与x轴有两个不同的交点;
(3)设抛物线顶点为P,若O、A、P三点共线(O为坐标原点),求b的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知△ABC的三个角是∠A,∠B,∠C ,它们所对的边分别是a,b,c.①c2-a2=b2;②∠A=![]() ∠B=
∠B=![]() ∠C;③c=
∠C;③c=![]() a=
a=![]() b;④a=2,b=2
b;④a=2,b=2 ![]() ,c=
,c=![]() .上述四个条件中,能判定△ABC 为直角三角形的有( )
.上述四个条件中,能判定△ABC 为直角三角形的有( )
A. 1个 B. 2个
C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(一)如下图①:把三个正方形摆成一定的形状。
问题(1):
若图中的三角形△DEF为直角三角形,P的面积为9,Q的面积为15,则M的面积为( ).
问题(2):
若P的面积为36cm2,Q的面积为64cm2,同时M的面积为100cm2,则△DEF为( )三角形.
(二)图形变化:
如图②,分别以直角△ABC的三边为直径向三角形外作三个半圆,你能找出这三个半圆的面积之间有什么关系吗?请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在菱形ABCD中,∠ABC=60°,AB=1,点P是这个菱形内部或边上的一点,若以点P、B、C为顶点的三角形是等腰三角形,则P、D(P、D两点不重合)两点间的最短距离为多少?( )
A. 1 B. ![]() C. 2 D.
C. 2 D. ![]() -1
-1
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com