Question

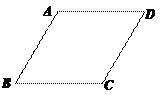
【题目】如图，在菱形ABCD中，∠ABC=60°，AB=1，点P是这个菱形内部或边上的一点，若以点P、B、C为顶点的三角形是等腰三角形，则P、D（P、D两点不重合）两点间的最短距离为多少？（ ）

A. 1 B. C. 2 D. -1

Answer 1

【答案】D

【解析】分析：分三种情形讨论①若以边BC为底.②若以边PC为底.③若以边PB为底.分别求出PD的最小值,即可判断.

详解：:在菱形ABCD中,

∵∠ABC=60°，AB=1，

∴△ABC, △ACD都是等边三角形,

①若以边BC为底,则BC垂直平分线上(在菱形的边及其内部)的点满足题意,此时就转化为了“直线外一点与直线上所有点连线的线段中垂线段最短“,即当点P与点A重合时,PD值最小,最小值为1;

②若以边PB为底, ∠PCB为顶角,以点C为圆心,BC为半径作圆,则弧BD上的点A与点D均满足△PBC为等腰三角形,当点P与点D重合时,PD最小,显然不满足题意,故此种情况不存在;

③若以边PC为底, ∠PBC为顶角时,以点B为圆心,BC长为半径作圆,与BD相交于一点,则弧AC(除点C外)上的所有点都满足△PBC是等腰三角形,当点P在BD上时,PD最小.

∵四边形ABCD是菱形，∠ABC=60°，

∴AB=BC=CD=AD，∠ABC=∠ADC=60°，

∴△ABC，△ADC是等边三角形，

∴BO=DO=sin60 ×1=，

∴BD=2BO=2×=，

∴PD =BD-BP=-1.

∵-1<1,

∴PD的最小值为-1.