
【题目】如图,将正方形ABCD折叠,使顶点A与CD边上的一点H重合(H不与端点C,D重合),折痕交AD于点E,交BC于点F,边AB折叠后与边BC交于点G,如果正方形ABCD的边长为1,则△CHG的周长为__________

【答案】2
【解析】分析:设CH=x,DE=y,则DH=1-x,EH=1-y,然后利用正方形的性质和折叠可以证明△DEH∽△CHG,利用相似三角形的对应边成比例可以把CG,HG分别用x,y分别表示,△CHG的周长也用x,y表示,然后在Rt△DEH中根据勾股定理可以得到2x-x2=2y,进而求出△CHG的周长.
详解:设CH=x,DE=y,则DH=1-x,EH=1-y,
∵∠EHG=90°,
∴∠DHE+∠CHG=90°.
∵∠DHE+∠DEH=90°,
∴∠DEH=∠CHG,
又∵∠D=∠C=90°,
∴△DEH∽△CHG,
∴CG:DH=CH:DE=HG:EH,即CG:(1x)=x:y=HG:(1y),
∴CG=![]() ,HG=
,HG=![]() ,
,
∴△CMG的周长为=CH+CG+HG=![]() ,
,
在Rt△DEH中,DH2+DE2=EH2,
即(1-x)2+y2=(1-y)2,
整理得2x-x2=2y,
∴CH+HG+CG=![]() .
.
故答案为:2.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】已知抛物线y=2x2+bx+c经过点A(2,-1) .
(1)若抛物线的对称轴为x=1,求b,c的值;
(2)求证:抛物线与x轴有两个不同的交点;
(3)设抛物线顶点为P,若O、A、P三点共线(O为坐标原点),求b的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2017年12月3日至5日,第四届世界互联网大会在浙江省乌镇举行.会议期间,某公司的无人超市,让人们感受到互联网新零售带来的全新体验.小张购买了钥匙扣和毛绒玩具两种商品共15件,离开超市后,收到短信显示,购买钥匙扣支付240元,购买毛绒玩具支付180元.已知毛绒玩具的单价是钥匙扣单价的1.5倍,那么钥匙扣和毛绒玩具的单价各是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某数学兴趣小组同学进行测量大树CD高度的综合实践活动,如右图,在点A处测得直立于地面的大树顶端C的仰角为45°,然后沿在同一剖面的斜坡AB行走13米至坡顶B处,然后再沿水平方向行走6米至大树脚底点D处,斜面AB的坡度(或坡比)i=1∶2.4,那么大树CD的高度约为多少?( )

A. 18米 B. 13米 C. 12米 D. 5米
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在菱形ABCD中,∠ABC=60°,AB=1,点P是这个菱形内部或边上的一点,若以点P、B、C为顶点的三角形是等腰三角形,则P、D(P、D两点不重合)两点间的最短距离为多少?( )
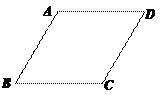
A. 1 B. ![]() C. 2 D.
C. 2 D. ![]() -1
-1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(2013年四川南充3分)如图,把矩形ABCD沿EF翻折,点B恰好落在AD边的B′处,若AE=2,DE=6,∠EFB=60°,则矩形ABCD的面积是【 】
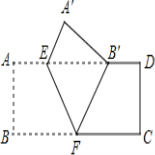
A.12 B. 24 C. 12![]() D. 16
D. 16![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是半圆O的直径,AB=2,射线AM、BN为半圆O的切线.在AM上取一点D,连接BD交半圆于点C,连接AC.过O点作BC的垂线OE,垂足为点E,与BN相交于点F.过D点作半圆O的切线DP,切点为P,与BN相交于点Q.
(1)若△ABD≌△BFO,求BQ的长;
(2)求证:FQ=BQ

查看答案和解析>>
科目:初中数学 来源: 题型:
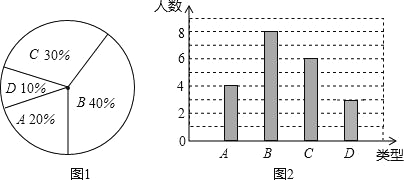
【题目】某校260名学生参加植树活动,要求每人植4~7棵,活动结束后随机抽查了若干名学生每人的植树量,并分为四种类型, A:4棵;B:5棵;C:6棵;D:7棵,将各类的人数绘制成扇形图(如图1)和条形图(如图2),请回答下列问题:
(1)在这次调查中D类型有多少名学生?
(2)写出被调查学生每人植树量的众数、中位数;
(3)求被调查学生每人植树量的平均数,并估计这260名学生共植树多少棵?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,正方形网格中,△ABC为格点三角形(即三角形的顶点都在格点上).

(1)把△ABC沿BA方向平移后,点A移到点A1,在网格中画出平移后得到的△A1B1C1;
(2)把△A1B1C1绕点A1按逆时针方向旋转90°,在网格中画出旋转后的△A1B2C2;
(3)如果网格中小正方形的边长为1,求点B经过(1)、(2)变换的路径总长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com