
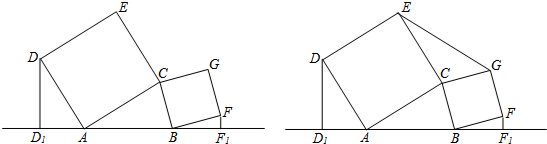
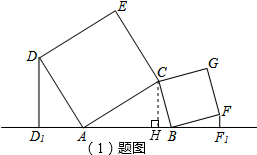
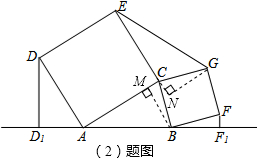
 (1)证明:如图,过点C作CH⊥AB于H,
(1)证明:如图,过点C作CH⊥AB于H,
|
|


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
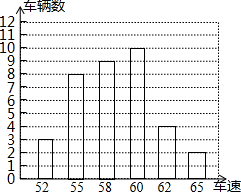 为了了解汽车司机遵守交通法规的意识,小明的学习小组成员协助交通警察在某路口统计的某个时段来往汽车的车速(单位:km/h)情况如图所示.根据统计图分析,这组车速数据的众数和中位数分别是( )
为了了解汽车司机遵守交通法规的意识,小明的学习小组成员协助交通警察在某路口统计的某个时段来往汽车的车速(单位:km/h)情况如图所示.根据统计图分析,这组车速数据的众数和中位数分别是( )| A、60km/h,60km/h |
| B、58km/h,60km/h |
| C、60km/h,58km/h |
| D、58km/h,58km/h |
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
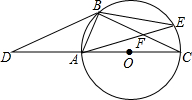 如图,点D是⊙O的直径CA延长线上一点,点B在⊙O上,且∠DBA=∠BCD.
如图,点D是⊙O的直径CA延长线上一点,点B在⊙O上,且∠DBA=∠BCD.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com