
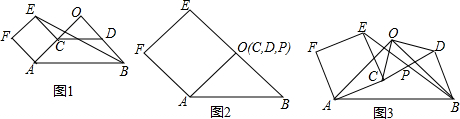
分析 (1)根据已知直接证明有一个直角且邻边相等即可;
(2)通过证明三角形CEP和三角形DBP全等,结合等量代换即可证明;
(3)与(2)同理可证EC=DB,EC∥DB,进一步证明△AOC≌△BOD,结合等量代换和平行线的性质即可解答.
解答 解:(1)正方形;
如图2,
∵△AOB是等腰直角三角形,
∴∠AOE=90°,AO=BO,
∵OE=BO,
∴AO=OE,
∴平行四边形ACEF是正方形;
(2)如图1,
∵P是CD的中点,
∴PC=PD,
在△CPE和△BPD中,
$\left\{\begin{array}{l}{PC=PE}\\{∠CPE=∠DPB}\\{PE=PB}\end{array}\right.$,
∴△CPE≌△BPD,
∴EC=DB,
∵OA=OB,OC=OD,
∴AC=DB,
∴EC=AC,
∴平行四边形ACEF是菱形,
∵△CPE≌△BPD,
∴∠CEP=∠DBP,
∴EC∥OB,
∵∠O=90°,
∴∠ACE=90°,
∴菱形ACEF是正方形;
(3)如图3,
与(2)同理可证△CPE≌△BPD,
∴EC=DB,EC∥DB,
∵∠AOC+∠COB=∠COB+∠DOB=90°,
∴∠AOC=∠DOB,
在△AOC和△BOD中,
$\left\{\begin{array}{l}{OA=OB}\\{∠AOC=∠BOD}\\{OC=OD}\end{array}\right.$,
∴△AOC≌△BOD,
∵∠COD=90°,
∴△AOC可以看作△BOD顺时针绕点O旋转90°得到,
∴AC⊥DB,AC=DB,
∴EC=AC,
∴平行四边形ACEF是菱形,
∵EC∥DB,
∴AC⊥EC,
∴菱形ACEF是正方形.
点评 此题主要考查几何变换中的旋转,在旋转中找到并证明全等三角形,并灵活运用全等三角形的性质进行推理是解题的关键.


科目:初中数学 来源: 题型:解答题
| 销售单价x(元/件) | … | 20 | 30 | 40 | 50 | 60 | … |
| 每天销售量(y件) | … | 500 | 400 | 300 | 200 | 100 | … |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 9.98×107 | B. | 9.98×108 | C. | O.998×109 | D. | 99.8×107 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 (1)解不等式组:$\left\{\begin{array}{l}{2x-1>x+1}\\{x+8>4x-1}\end{array}\right.$,并把解集在数轴上表示出来.
(1)解不等式组:$\left\{\begin{array}{l}{2x-1>x+1}\\{x+8>4x-1}\end{array}\right.$,并把解集在数轴上表示出来.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,⊙O是以原点为圆心,2为半径的圆,点P是直线y=-x+4上的一点,过点P作⊙O的一条切线PQ,Q为切点,则切线长PQ的最小值为2.
如图,⊙O是以原点为圆心,2为半径的圆,点P是直线y=-x+4上的一点,过点P作⊙O的一条切线PQ,Q为切点,则切线长PQ的最小值为2.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com