
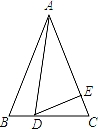
如图,在△ABC中,AB=AC=8,BC=6,点D为BC上一点,BD=2.过点D作射线DE交AC于点E,使∠ADE=∠B.
(1)求证: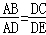 ;
;
(2)求线段EC的长度.
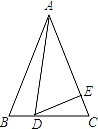
【考点】相似三角形的判定与性质.
【分析】(1)由条件可得到∠BAD=∠EDC,可证明△ABD∽△DCE,即可得到结论;
(2)由相似三角形的性质可得到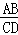 =
=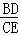 ,代入可求得EC.
,代入可求得EC.
【解答】解:(1)∵AB=AC,
∴∠B=∠C,
∵∠ADC是△ABD的一个外角,
∴∠ACD=∠B+∠BAD=∠ADE+∠EDC,
又∵∠B=∠ADE,
∴∠BAD=∠EDC,
∴△ABD∽△DCE,
∴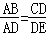 ;
;
(2)∵△ABD∽△DCE,
∴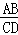 =
=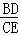 ,
,
∵BC=6,BD=2,
∴CD=4,
∴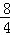 =
=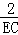 ,
,
解得EC=1.
【点评】本题主要考查相似三角形的判定和性质,由条件得到∠BAD=∠DCE证得△ABD∽△DCE是解题的关键.


 特高级教师点拨系列答案
特高级教师点拨系列答案科目:初中数学 来源: 题型:
以下关于x的方程一定是一元二次方程的是( )
A.ax2+bx+c=0 B.2(x﹣1)2=2x2+2
C.(k+1)x2+3x=2 D.(k2+1)x2﹣2x+1=0
查看答案和解析>>
科目:初中数学 来源: 题型:
已知点A(x1,y1),B(x2,y2)是反比例函数y=﹣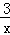 的图象上的两点,若x1<0<x2,则下列结论正确的是( )
的图象上的两点,若x1<0<x2,则下列结论正确的是( )
A.y1<0<y2 B.y2<0<y1 C.y1<y2<0 D.y2<y1<0
查看答案和解析>>
科目:初中数学 来源: 题型:
为了更好保护水资源,造福人类,某工厂计划建一个容积V(m3)一定的污水处理池,池的底面积S(m2)与其深度h(m)满足关系式:V=Sh(V≠0),则S关于h的函数图象大致是( )
A.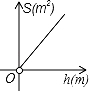 B.
B.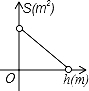 C.
C.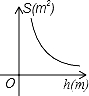 D.
D.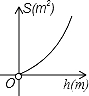
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,AB是⊙O的直径,CD与⊙O相切于点C,DA⊥AB,DO及DO的延长线与⊙O分别相交于点E、F,EB与CF相交于点G.
(1)求证:DA=DC;
(2)⊙O的半径为3,AC= ,求GC的长.
,求GC的长.
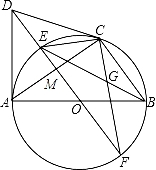
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com