
分析 先计算出2015是第1008个数,然后判断第1008个数在第几组,再判断是这一组的第几个数即可.
解答 解:2015是第$\frac{2015+1}{2}$=1008个数,
设2015在第n组,则1+3+5+7+…+(2n-1)≥1008,
即n2≥1008,
解得:n≥$\sqrt{1008}$,
当n=31时,1+3+5+7+…+61=961;
当n=32时,1+3+5+7+…+63=1024;
故第1008个数在第32组,
第1024个数为:2×1024-1=2047,
第32组的第一个数为:2×962-1=1923,
则2015是($\frac{2015-1923}{2}$+1)=47个数.
故A2015=(32,47).
故答案为:(32,47).
点评 此题考查数字的变化规律,找出数字之间的运算规律,利用规律解决问题.


 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案科目:初中数学 来源: 题型:解答题
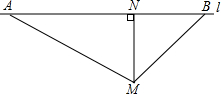 如图,根据道路管理规定,在某笔直的大道AB上行驶的车辆,限速60千米/时,已知测速站点M距大道AB的距离MN为30米,现有一辆汽车从A向B方向匀速行驶,测得此车从A点行驶到B点所用时间危机6秒,∠AMN=60°,∠BMN=45°.
如图,根据道路管理规定,在某笔直的大道AB上行驶的车辆,限速60千米/时,已知测速站点M距大道AB的距离MN为30米,现有一辆汽车从A向B方向匀速行驶,测得此车从A点行驶到B点所用时间危机6秒,∠AMN=60°,∠BMN=45°.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
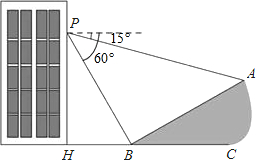 如图,小明在大楼30米高(即PH=30米)窗口P处进行观测,测得山坡上A处的俯角为15°,山脚B处的俯角为60°,已知该山坡的坡度i(即tan∠ABC)为1:$\sqrt{3}$,点P,H,B,C,A在同一个平面上,点H、B、C在同一条直线上,且PH丄HC.求A、B两点间的距离.(结果精确到1米,参考数据:$\sqrt{3}$≈1.732).
如图,小明在大楼30米高(即PH=30米)窗口P处进行观测,测得山坡上A处的俯角为15°,山脚B处的俯角为60°,已知该山坡的坡度i(即tan∠ABC)为1:$\sqrt{3}$,点P,H,B,C,A在同一个平面上,点H、B、C在同一条直线上,且PH丄HC.求A、B两点间的距离.(结果精确到1米,参考数据:$\sqrt{3}$≈1.732).查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{12}{13}$ | B. | $\frac{5}{12}$ | C. | $\frac{13}{12}$ | D. | $\frac{12}{5}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
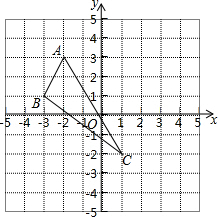 已知△ABC在平面直角坐标系中的位置如图所示
已知△ABC在平面直角坐标系中的位置如图所示查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com