
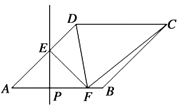
【题目】如图,在菱形ABCD中,∠DAB=45°,AB=4,点P为线段AB上一动点(不与点A重合),过点P作PE⊥AB交射线AD于点E,沿PE将△APE折叠,点A的对称点为点F,连接EF,DF,CF,当△CDF为等腰三角形时,AP的长为________.
【答案】2,![]() 或
或![]()
【解析】
根据题意分DF=CD、CF=CD或FD=FC三种情况先得出相应的图形,由此进一步结合相关信息加以分析即可.
如图1,当DF=CD时,点F在![]() 点处,作DN⊥AB于点N,
点处,作DN⊥AB于点N,
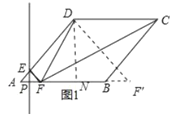
∵四边形ABCD是菱形,AB=4,
∴CD=AD=4,
在Rt△AND中,
∵∠DAN=45°,AD=4,
∴DN=AN=![]() ,
,
又∵DA=D![]() ,且DN⊥AB,
,且DN⊥AB,
∴N![]() =AN=
=AN=![]() ,
,
∴AP=![]() ;
;
如图2,当CF=CD=4时,点F与点B重合或在![]() 点处,
点处,
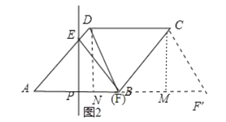
①点F与点B重合时,则PE是AB的垂直平分线,
∴AP=![]() ;
;
②点F在![]() 点处时,过点C作CM⊥AB于点M,
点处时,过点C作CM⊥AB于点M,
易得:∠DAB=∠![]() =45°,CB=
=45°,CB=![]() =4,
=4,
∴CM=![]() =BM=
=BM=![]() ,
,
∴![]() =
=![]() ,
,
∴AP=![]() ,
,
此时点E不在线段AD上,舍去;
如图3,当FD=FC时,过点F作FQ⊥CD于点Q,交BC于点G,
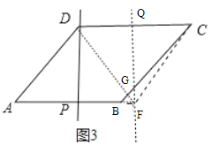
则:CQ=DQ=QG=2,FQ=![]() ,
,
∴BF=GF=![]() ,
,
∴AF=![]() ,
,
∴AP=![]() ;
;
综上所述,AP的长度为:2,![]() 或
或![]() ,
,
故答案为:2,![]() 或
或![]() .
.


科目:初中数学 来源: 题型:
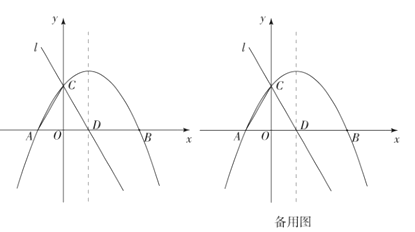
【题目】综合与探究:在平面直角坐标系![]() 中,已知抛物线
中,已知抛物线![]() 与
与![]() 轴交于
轴交于![]() ,
,![]() 两点(点
两点(点![]() 在点
在点![]() 的右侧),与
的右侧),与![]() 轴交于点
轴交于点![]() ,它的对称轴与
,它的对称轴与![]() 轴交于点
轴交于点![]() ,直线
,直线![]() 经过
经过![]() ,
,![]() 两点,连接
两点,连接![]() .
.
(1)求![]() ,
,![]() 两点的坐标及直线
两点的坐标及直线![]() 的函数表达式;
的函数表达式;
(2)探索直线![]() 上是否存在点
上是否存在点![]() ,使
,使![]() 为直角三角形,若存在,求出点
为直角三角形,若存在,求出点![]() 的坐标;若不存在,说明理由;
的坐标;若不存在,说明理由;
(3)若点![]() 是直线
是直线![]() 上的一个动点,试探究在抛物线上是否存在点
上的一个动点,试探究在抛物线上是否存在点![]() :
:
①使以点![]() ,
,![]() ,
,![]() ,
,![]() 为顶点的四边形为菱形,若存在,请直接写出点
为顶点的四边形为菱形,若存在,请直接写出点![]() 的坐标;若不存在,说明理由;
的坐标;若不存在,说明理由;
②使以点![]() ,
,![]() ,
,![]() ,
,![]() 为顶点的四边形为矩形,若存在,请直接写出点
为顶点的四边形为矩形,若存在,请直接写出点![]() 的坐标;若不存在,说明理由.
的坐标;若不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
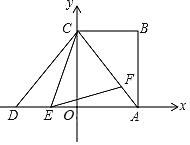
【题目】如图,矩形ABCD的顶点A、C在平面直角坐标系的坐标轴上,AB=4,CB=3,点D与点A关于y轴对称,点E、F分别是线段DA、AC上的动点(点E不与A、D重合),且∠CEF=∠ACB,若△EFC为等腰三角形,则点E的坐标为______.
查看答案和解析>>
科目:初中数学 来源: 题型:
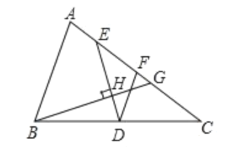
【题目】如图,在![]() 中,AB<AC,点D、F分别为BC、AC的中点,E点在边AC上,连接DE,过点B作DE的垂线交AC于点G,垂足为点H,且
中,AB<AC,点D、F分别为BC、AC的中点,E点在边AC上,连接DE,过点B作DE的垂线交AC于点G,垂足为点H,且![]() 与四边形ABDE的周长相等,设AC=b,AB=c.
与四边形ABDE的周长相等,设AC=b,AB=c.
(1)求线段CE的长度;
(2)求证:DF=EF;
(3)若![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
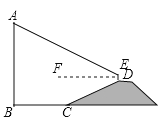
【题目】如图,![]() 是垂直于水平面的建筑物,为测量
是垂直于水平面的建筑物,为测量![]() 的高度,小红从建筑物底端
的高度,小红从建筑物底端![]() 出发,沿水平方向行走了52米到达点
出发,沿水平方向行走了52米到达点![]() ,然后沿斜坡
,然后沿斜坡![]() 前进,到达坡顶
前进,到达坡顶![]() 点处,
点处,![]() .在点
.在点![]() 处放置测角仪,测角仪支架
处放置测角仪,测角仪支架![]() 高度为0.8米,在
高度为0.8米,在![]() 点处测得建筑物顶端
点处测得建筑物顶端![]() 点的仰角
点的仰角![]() 为
为![]() (点
(点![]() ,
,![]() ,
,![]() ,
,![]() 在同一平面内),斜坡
在同一平面内),斜坡![]() 的坡度(或坡比)
的坡度(或坡比)![]() ,求建筑物
,求建筑物![]() 的高度.(精确到个位)(参考数据:
的高度.(精确到个位)(参考数据:![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某科技公司研发出一款多型号的智能手表,一家代理商出售该公司的![]() 型智能手表,去年销售总额为80000元,今年
型智能手表,去年销售总额为80000元,今年![]() 型智能手表的售价每只比去年降了600元,若今年售出的数量与去年相同的情况下,今年的销售总额将比去年减少
型智能手表的售价每只比去年降了600元,若今年售出的数量与去年相同的情况下,今年的销售总额将比去年减少![]() .
.
(1)求今年![]() 型智能手表每只售价多少元?
型智能手表每只售价多少元?
(2)今年这家代理商准备新进一批![]() 型智能手表和
型智能手表和![]() 型智能手表共100只,它们的进货价与销售价格如下表所示,若
型智能手表共100只,它们的进货价与销售价格如下表所示,若![]() 型智能手表进货量不超过
型智能手表进货量不超过![]() 型智能手表进货量的3倍,所进智能手表可全部售完,请你设计出进货方案,使这批智能手表获利最多,并求出最大利润是多少元?
型智能手表进货量的3倍,所进智能手表可全部售完,请你设计出进货方案,使这批智能手表获利最多,并求出最大利润是多少元?
|
| |
进价 | 1300元/只 | 1500元/只 |
售价 | 今年的售价 | 2300元/只 |
查看答案和解析>>
科目:初中数学 来源: 题型:
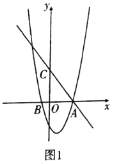
【题目】已知:如图1,抛物线![]() 是由抛物线
是由抛物线![]() 向右平移1个单位,再向下平移4个单位得到的,
向右平移1个单位,再向下平移4个单位得到的,![]() 与
与![]() 轴交于
轴交于![]() ,
,![]() 两点(
两点(![]() 在
在![]() 的右侧),直线
的右侧),直线![]() 经过点
经过点![]() ,与
,与![]() 轴交于
轴交于![]() 点.
点.
(1)分别求出![]() ,
,![]() ,
,![]() 的值;
的值;
(2)如图2,已知![]() 点是线段
点是线段![]() 上任一点(不与
上任一点(不与![]() ,
,![]() 重合),过
重合),过![]() 点作
点作![]() 轴垂线,交抛物线
轴垂线,交抛物线![]() 于
于![]() 点.当
点.当![]() 在何处时,四边形
在何处时,四边形![]() 面积最大,求出此时
面积最大,求出此时![]() 点坐标及四边形
点坐标及四边形![]() 面积的最大值.
面积的最大值.

查看答案和解析>>
科目:初中数学 来源: 题型:
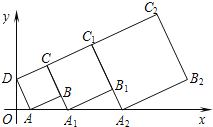
【题目】在平面坐标系中,第1个正方形ABCD的位置如图所示,点A的坐标为(3,0),点D的坐标为(0,4),延长CB交x轴于点A1,作第2个正方形A1B1C1C,延长C1B1交x轴于点A2;作第3个正方形A2B2C2C1,…按这样的规律进行下去,第5个正方形的边长为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系内,以原点O为圆心,1为半径作圆,点P在直线![]() 上运动,过点P作该圆的一条切线,切点为A,则PA的最小值为
上运动,过点P作该圆的一条切线,切点为A,则PA的最小值为![]()
![]()
A. 3 B. 2 C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com