
ЁОЬтФПЁПФГПЦММЙЋЫОбаЗЂГівЛПюЖраЭКХЕФжЧФмЪжБэЃЌвЛМвДњРэЩЬГіЪлИУЙЋЫОЕФ![]() аЭжЧФмЪжБэЃЌШЅФъЯњЪлзмЖюЮЊ80000дЊЃЌНёФъ
аЭжЧФмЪжБэЃЌШЅФъЯњЪлзмЖюЮЊ80000дЊЃЌНёФъ![]() аЭжЧФмЪжБэЕФЪлМлУПжЛБШШЅФъНЕСЫ600дЊЃЌШєНёФъЪлГіЕФЪ§СПгыШЅФъЯрЭЌЕФЧщПіЯТЃЌНёФъЕФЯњЪлзмЖюНЋБШШЅФъМѕЩй
аЭжЧФмЪжБэЕФЪлМлУПжЛБШШЅФъНЕСЫ600дЊЃЌШєНёФъЪлГіЕФЪ§СПгыШЅФъЯрЭЌЕФЧщПіЯТЃЌНёФъЕФЯњЪлзмЖюНЋБШШЅФъМѕЩй![]() .
.
ЃЈ1ЃЉЧѓНёФъ![]() аЭжЧФмЪжБэУПжЛЪлМлЖрЩйдЊЃП
аЭжЧФмЪжБэУПжЛЪлМлЖрЩйдЊЃП
ЃЈ2ЃЉНёФъетМвДњРэЩЬзМБИаТНјвЛХњ![]() аЭжЧФмЪжБэКЭ
аЭжЧФмЪжБэКЭ![]() аЭжЧФмЪжБэЙВ100жЛЃЌЫќУЧЕФНјЛѕМлгыЯњЪлМлИёШчЯТБэЫљЪОЃЌШє
аЭжЧФмЪжБэЙВ100жЛЃЌЫќУЧЕФНјЛѕМлгыЯњЪлМлИёШчЯТБэЫљЪОЃЌШє![]() аЭжЧФмЪжБэНјЛѕСПВЛГЌЙ§
аЭжЧФмЪжБэНјЛѕСПВЛГЌЙ§![]() аЭжЧФмЪжБэНјЛѕСПЕФ3БЖЃЌЫљНјжЧФмЪжБэПЩШЋВПЪлЭъЃЌЧыФуЩшМЦГіНјЛѕЗНАИЃЌЪЙетХњжЧФмЪжБэЛёРћзюЖрЃЌВЂЧѓГізюДѓРћШѓЪЧЖрЩйдЊЃП
аЭжЧФмЪжБэНјЛѕСПЕФ3БЖЃЌЫљНјжЧФмЪжБэПЩШЋВПЪлЭъЃЌЧыФуЩшМЦГіНјЛѕЗНАИЃЌЪЙетХњжЧФмЪжБэЛёРћзюЖрЃЌВЂЧѓГізюДѓРћШѓЪЧЖрЩйдЊЃП
|
| |
НјМл | 1300дЊ/жЛ | 1500дЊ/жЛ |
ЪлМл | НёФъЕФЪлМл | 2300дЊ/жЛ |
ЁОД№АИЁПЃЈ1ЃЉНёФъ![]() аЭжЧФмЪжБэУПжЛЪлМл1800дЊЃЛЃЈ2ЃЉНјЛѕЗНАИЮЊаТНј
аЭжЧФмЪжБэУПжЛЪлМл1800дЊЃЛЃЈ2ЃЉНјЛѕЗНАИЮЊаТНј![]() аЭЪжБэ25жЛЃЌаТНј
аЭЪжБэ25жЛЃЌаТНј![]() аЭЪжБэ75жЛЃЌетХњжЧФмЪжБэЛёРћзюЖрЃЌзюДѓРћШѓЪЧ72500дЊЃЎ
аЭЪжБэ75жЛЃЌетХњжЧФмЪжБэЛёРћзюЖрЃЌзюДѓРћШѓЪЧ72500дЊЃЎ
ЁОНтЮіЁП
ЃЈ1ЃЉЩшНёФъAаЭжЧФмЪжБэУПжЛЪлМлxдЊЃЌдђШЅФъЪлМлУПжЛЮЊЃЈx+600ЃЉдЊЃЌгЩТєГіЕФЪ§СПЯрЭЌНЈСЂЗНГЬЧѓГіЦфНтМДПЩЃЛ
ЃЈ2ЃЉЩшНёФъаТНјAаЭaжЛЃЌдђBаЭЃЈ100-aЃЉжЛЃЌЛёРћyдЊЃЌгЩЬѕМўБэЪОГіWгыaжЎМфЕФЙиЯЕЪНЃЌгЩaЕФШЁжЕЗЖЮЇОЭПЩвдЧѓГіWЕФзюДѓжЕЃЎ
НтЃКЃЈ1ЃЉЩшНёФъ![]() аЭжЧФмЪжБэУПжЛЪлМл
аЭжЧФмЪжБэУПжЛЪлМл![]() дЊЃЌШЅФъЪлМлУПжЛЮЊ
дЊЃЌШЅФъЪлМлУПжЛЮЊ![]() дЊЃЌ
дЊЃЌ
ИљОнЬтвтЕУЃЌ![]()
НтЕУЃК![]() ЃЌ
ЃЌ
ОМьбщЃЌ![]() ЪЧдЗНГЬЕФИљЃЌЧвЗћКЯЬтвтЃЌ
ЪЧдЗНГЬЕФИљЃЌЧвЗћКЯЬтвтЃЌ
Д№ЃКНёФъ![]() аЭжЧФмЪжБэУПжЛЪлМл1800дЊЃЎ
аЭжЧФмЪжБэУПжЛЪлМл1800дЊЃЎ
ЃЈ2ЃЉЩшаТНј![]() аЭЪжБэ
аЭЪжБэ![]() жЛЃЌдђаТНј
жЛЃЌдђаТНј![]() аЭЪжБэ
аЭЪжБэ![]() жЛЃЌЫљНјжЧФмЪжБэШЋВПЪлЭъРћШѓЪЧ
жЛЃЌЫљНјжЧФмЪжБэШЋВПЪлЭъРћШѓЪЧ![]() дЊЃЌ
дЊЃЌ
ИљОнЬтвтЕУЃЌ![]() ЃЌ
ЃЌ
Ёп![]() ЃЌ
ЃЌ
Ёр![]() ЃЌ
ЃЌ
Ёп![]() ЃЌ
ЃЌ![]() Ыц
Ыц![]() ЕФдіДѓЖјМѕаЁЃЌ
ЕФдіДѓЖјМѕаЁЃЌ
ЁрЕБ![]() ЪБЃЌ
ЪБЃЌ![]() ЃЌ
ЃЌ![]() ЃЈдЊЃЉЃЌ
ЃЈдЊЃЉЃЌ
ДЫЪБЃЌНјЛѕЗНАИЮЊаТНј![]() аЭЪжБэ 25жЛЃЌаТНј
аЭЪжБэ 25жЛЃЌаТНј![]() аЭЪжБэ75жЛЃЌ
аЭЪжБэ75жЛЃЌ
Д№ЃКНјЛѕЗНАИЮЊаТНј![]() аЭЪжБэ25жЛЃЌаТНј
аЭЪжБэ25жЛЃЌаТНј![]() аЭЪжБэ75жЛЃЌетХњжЧФмЪжБэЛёРћзюЖрЃЌзюДѓРћШѓЪЧ72500дЊЃЎ
аЭЪжБэ75жЛЃЌетХњжЧФмЪжБэЛёРћзюЖрЃЌзюДѓРћШѓЪЧ72500дЊЃЎ



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЪ§бЇЛюЖЏПЮЩЯЃЌРЯЪІЬсГіЮЪЬтЃКШчЭМЃЌгавЛеХГЄ4dmЃЌПэ3dmЕФГЄЗНаЮжНАхЃЌдкжНАхЕФЫФИіНЧВУШЅЫФИіЯрЭЌЕФаЁе§ЗНаЮЃЌШЛКѓАбЫФБпелЦ№РДЃЌзіГЩвЛИіЮоИЧЕФКазгЃЌЮЪаЁе§ЗНаЮЕФБпГЄЮЊЖрЩйЪБЃЌКазгЕФЬхЛ§зюДѓЃЎ

ЯТУцЪЧЬНОПЙ§ГЬЃЌЧыВЙГфЭъећЃК
ЃЈ1ЃЉЩшаЁе§ЗНаЮЕФБпГЄЮЊx dmЃЌЬхЛ§ЮЊy dm3ЃЌИљОнГЄЗНЬхЕФЬхЛ§ЙЋЪНЕУЕНyКЭxЕФЙиЯЕЪНЃК ЃЛ
ЃЈ2ЃЉШЗЖЈздБфСПxЕФШЁжЕЗЖЮЇЪЧ ЃЛ
ЃЈ3ЃЉСаГіyгыxЕФМИзщЖдгІжЕ.
x/dm | Ё |
|
|
|
|
|
|
|
|
|
| Ё |
y/dm3 | Ё | 1.3 | 2.2 | 2.7 | m | 3.0 | 2.8 | 2.5 | n | 1.5 | 0.9 | Ё |
ЃЈ4ЃЉдкЯТУцЕФЦНУцжБНЧзјБъЯЕ![]() жаЃЌУшГіВЙШЋКѓЕФБэжаИїЖдЖдгІжЕЮЊзјБъЕФЕуЃЌВЂЛГіИУКЏЪ§ЕФЭМЯѓШчЯТЭМЃЛ
жаЃЌУшГіВЙШЋКѓЕФБэжаИїЖдЖдгІжЕЮЊзјБъЕФЕуЃЌВЂЛГіИУКЏЪ§ЕФЭМЯѓШчЯТЭМЃЛ
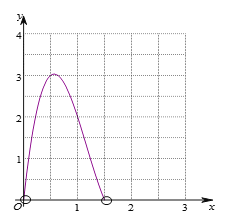
НсКЯЛГіЕФКЏЪ§ЭМЯѓЃЌНтОіЮЪЬтЃК
ЕБаЁе§ЗНаЮЕФБпГЄдМЮЊ dmЪБЃЌЃЈБЃСє1ЮЛаЁЪ§ЃЉЃЌКазгЕФЬхЛ§зюДѓЃЌзюДѓжЕдМЮЊ dm3ЃЎЃЈБЃСє1ЮЛаЁЪ§ЃЉ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЫљЪОЃЌЁїABCжаЃЌЁЯB=90ЁуЃЌAB=6cmЃЌBC=8cmЃЎ
ЃЈ1ЃЉЕуPДгЕуAПЊЪМбиABБпЯђBвд1cm/sЕФЫйЖШвЦЖЏЃЌЕуQДгBЕуПЊЪМбиBCБпЯђЕуCвд2cm/sЕФЫйЖШвЦЖЏЃЎШчЙћPЃЌQЗжБ№ДгAЃЌBЭЌЪБГіЗЂЃЌОЙ§МИУыЃЌЪЙЁїPBQЕФУцЛ§ЕШгк8cm2ЃП
ЃЈ2ЃЉЕуPДгЕуAПЊЪМбиABБпЯђBвд1cm/sЕФЫйЖШвЦЖЏЃЌЕуQДгBЕуПЊЪМбиBCБпЯђЕуCвд2cm/sЕФЫйЖШвЦЖЏЃЎШчЙћPЃЌQЗжБ№ДгAЃЌBЭЌЪБГіЗЂЃЌЯпЖЮPQФмЗёНЋЁїABCЗжГЩУцЛ§ЯрЕШЕФСНВПЗжЃПШєФмЃЌЧѓГідЫЖЏЪБМфЃЛШєВЛФмЫЕУїРэгЩЃЎ
ЃЈ3ЃЉШєPЕубиЩфЯпABЗНЯђДгAЕуГіЗЂвд1cm/sЕФЫйЖШвЦЖЏЃЌЕуQбиЩфЯпCBЗНЯђДгCЕуГіЗЂвд2cm/sЕФЫйЖШвЦЖЏЃЌPЃЌQЭЌЪБГіЗЂЃЌЮЪМИУыКѓЃЌЁїPBQЕФУцЛ§ЮЊ1ЃП

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкЫФБпаЮABCDжаЃЌЖдНЧЯпACЦНЗжЁЯDABЃЌЁЯABD=52ЁуЃЌЁЯABC=116ЁуЃЌЁЯACB=ІСЁуЃЌдђЁЯBDCЕФЖШЪ§ЮЊЃЈЁЁЁЁЃЉ

A. ІС B. ![]() ІС C. 90ЉІС D. 90Љ
ІС C. 90ЉІС D. 90Љ![]() ІС
ІС
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁП2017Фъ12дТЃЌЦьЭХЮЏКХейИїаЃзщжЏПЊеЙОшдљвТЮяЕФЁАХЏЖЌааЖЏЁБ![]() ФГаЃЦпФъМЖСљИіАрВЮМгСЫетДЮОшдљЛюЖЏЃЌШєУПАрОшдљвТЮявд100МўЮЊЛљзМЃЌГЌЙ§ЕФМўЪ§гУе§Ъ§БэЪОЃЌВЛзуЕФМўЪ§гУИКЪ§БэЪОЃЌМЧТМШчЯТЃК
ФГаЃЦпФъМЖСљИіАрВЮМгСЫетДЮОшдљЛюЖЏЃЌШєУПАрОшдљвТЮявд100МўЮЊЛљзМЃЌГЌЙ§ЕФМўЪ§гУе§Ъ§БэЪОЃЌВЛзуЕФМўЪ§гУИКЪ§БэЪОЃЌМЧТМШчЯТЃК
АрМЖ | вЛАр | ЖўАр | Ш§Ар | ЫФАр | ЮхАр | СљАр |
ШЫЪ§ | 40 | 43 | 45 | 44 | 40 | 38 |
МўЪ§ |
|
|
|
|
|
|
![]() ОшдљвТЮязюЖрЕФАрБШзюЩйЕФАрЖрЖрЩйМўЃП
ОшдљвТЮязюЖрЕФАрБШзюЩйЕФАрЖрЖрЩйМўЃП
![]() ИУаЃЦпФъМЖбЇЩњЙВОшдљЖрЩйМўвТЮяЃПИУаЃЦпФъМЖбЇЩњЦНОљУПШЫОшдљЖрЩйМўвТЮяЃП
ИУаЃЦпФъМЖбЇЩњЙВОшдљЖрЩйМўвТЮяЃПИУаЃЦпФъМЖбЇЩњЦНОљУПШЫОшдљЖрЩйМўвТЮяЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊЃКШчЭМЃЌдкЬнаЮABCDжаЃЌABЁЮCDЃЌЁЯD=90ЁуЃЌAD=CD=2ЃЌЕуEдкБпADЩЯЃЈВЛгыЕуAЁЂDжиКЯЃЉЃЌЁЯCEB=45ЁуЃЌEBгыЖдНЧЯпACЯрНЛгкЕуFЃЌЩшDE=xЃЎ
ЃЈ1ЃЉгУКЌxЕФДњЪ§ЪНБэЪОЯпЖЮCFЕФГЄЃЛ
ЃЈ2ЃЉШчЙћАбЁїCAEЕФжмГЄМЧзїCЁїCAEЃЌЁїBAFЕФжмГЄМЧзїCЁїBAFЃЌЩш![]() =yЃЌЧѓyЙигкxЕФКЏЪ§ЙиЯЕЪНЃЌВЂаДГіЫќЕФЖЈвхгђЃЛ
=yЃЌЧѓyЙигкxЕФКЏЪ§ЙиЯЕЪНЃЌВЂаДГіЫќЕФЖЈвхгђЃЛ
ЃЈ3ЃЉЕБЁЯABEЕФе§ЧажЕЪЧ![]() ЪБЃЌЧѓABЕФГЄЃЎ
ЪБЃЌЧѓABЕФГЄЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкЫФБпаЮABCDжаЃЌ![]() ЃЌ
ЃЌ![]() ЪЧ
ЪЧ![]() ЕФжаЕуЃЌ
ЕФжаЕуЃЌ![]() ЃЌДЙзуЮЊЕу
ЃЌДЙзуЮЊЕу![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌЕу
ЃЌЕу![]() ЪЧ
ЪЧ![]() БпЩЯвЛЖЏЕуЃЌЩш
БпЩЯвЛЖЏЕуЃЌЩш![]() ЕФГЄЮЊ
ЕФГЄЮЊ![]() .
.
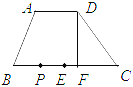
ЃЈ1ЃЉЕБ![]() ЕФжЕЮЊ________Лђ________ЪБЃЌвдЕу
ЕФжЕЮЊ________Лђ________ЪБЃЌвдЕу![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЮЊЖЅЕуЕФЫФБпаЮЮЊЦНааЫФБпаЮ.
ЮЊЖЅЕуЕФЫФБпаЮЮЊЦНааЫФБпаЮ.
ЃЈ2ЃЉЕу![]() дк
дк![]() БпЩЯдЫЖЏЕФЙ§ГЬжаЃЌвд
БпЩЯдЫЖЏЕФЙ§ГЬжаЃЌвд![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЮЊЖЅЕуЕФЫФБпаЮФмЗёЙЙГЩСтаЮЃПЪдЫЕУїРэгЩ.
ЮЊЖЅЕуЕФЫФБпаЮФмЗёЙЙГЩСтаЮЃПЪдЫЕУїРэгЩ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПНЋвЛОиаЮжНЦЌ![]() ЗХдкжБНЧзјБъЯЕжаЃЌ
ЗХдкжБНЧзјБъЯЕжаЃЌ![]() ЮЊдЕуЃЌЕу
ЮЊдЕуЃЌЕу![]() дк
дк![]() жсЩЯЃЌЕу
жсЩЯЃЌЕу![]() дк
дк![]() жсЩЯЃЌ
жсЩЯЃЌ![]() .
.
ЃЈ1ЃЉШчЭМ1ЃЌдк![]() ЩЯШЁвЛЕу
ЩЯШЁвЛЕу![]() ЃЌНЋ
ЃЌНЋ![]() би
би![]() елЕўЃЌЪЙ
елЕўЃЌЪЙ![]() ЕуТфдк
ЕуТфдк![]() БпЩЯЕФ
БпЩЯЕФ![]() ЕуДІЃЌЧѓжБЯп
ЕуДІЃЌЧѓжБЯп![]() ЕФНтЮіЪНЃЛ
ЕФНтЮіЪНЃЛ
ЃЈ2ЃЉШчЭМ2ЃЌдк![]() БпЩЯбЁШЁЪЪЕБЕФЕу
БпЩЯбЁШЁЪЪЕБЕФЕу![]() ЃЌНЋ
ЃЌНЋ![]() би
би![]() елЕўЃЌЪЙ
елЕўЃЌЪЙ![]() ЕуТфдк
ЕуТфдк![]() БпЩЯЕФЕу
БпЩЯЕФЕу![]() ДІЃЌЙ§
ДІЃЌЙ§![]() зї
зї![]() гкЕу
гкЕу![]() ЃЌНЛ
ЃЌНЛ![]() гк
гк![]() ЕуЃЌСЌНг
ЕуЃЌСЌНг![]() ЃЌХаЖЯЫФБпаЮ
ЃЌХаЖЯЫФБпаЮ![]() ЕФаЮзДЃЌВЂЫЕУїРэгЩЃЛ
ЕФаЮзДЃЌВЂЫЕУїРэгЩЃЛ
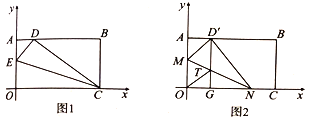
ЃЈ3ЃЉЁЂдкЃЈ2ЃЉЕФЬѕМўЯТЃЌШєЕу![]() зјБъ
зјБъ![]() ЃЌЕу
ЃЌЕу![]() дк
дк![]() жБЯпЩЯЃЌЮЪзјБъжсЩЯЪЧЗёДцдкЕу
жБЯпЩЯЃЌЮЪзјБъжсЩЯЪЧЗёДцдкЕу![]() ЃЌЪЙвд
ЃЌЪЙвд![]() ЮЊЖЅЕуЕФЫФБпаЮЪЧЦНааЫФБпаЮЃЌШєДцдкЃЌЧыжБНгаДГіЕу
ЮЊЖЅЕуЕФЫФБпаЮЪЧЦНааЫФБпаЮЃЌШєДцдкЃЌЧыжБНгаДГіЕу![]() зјБъЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩ.
зјБъЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПНтЗНГЬЃК
ЃЈ1ЃЉ3y2+1=2![]() y
y
ЃЈ2ЃЉЃЈ2x+1ЃЉ2=3ЃЈ2x+1ЃЉ
ЃЈ3ЃЉx2Љ4xЉ3=0ЃЈгУХфЗНЗЈЃЉ
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com