
【题目】数学活动课上,老师提出问题:如图,有一张长4dm,宽3dm的长方形纸板,在纸板的四个角裁去四个相同的小正方形,然后把四边折起来,做成一个无盖的盒子,问小正方形的边长为多少时,盒子的体积最大.

下面是探究过程,请补充完整:
(1)设小正方形的边长为x dm,体积为y dm3,根据长方体的体积公式得到y和x的关系式: ;
(2)确定自变量x的取值范围是 ;
(3)列出y与x的几组对应值.
x/dm | … |
|
|
|
|
|
|
|
|
|
| … |
y/dm3 | … | 1.3 | 2.2 | 2.7 | m | 3.0 | 2.8 | 2.5 | n | 1.5 | 0.9 | … |
(4)在下面的平面直角坐标系![]() 中,描出补全后的表中各对对应值为坐标的点,并画出该函数的图象如下图;
中,描出补全后的表中各对对应值为坐标的点,并画出该函数的图象如下图;
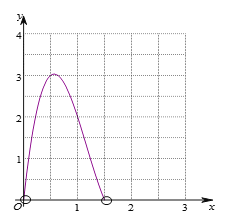
结合画出的函数图象,解决问题:
当小正方形的边长约为 dm时,(保留1位小数),盒子的体积最大,最大值约为 dm3.(保留1位小数)
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC是腰长为1的等腰直角三形,以Rt△ABC的斜边AC为直角边,画第二个等腰Rt△ACD,再以Rt△ACD的斜边AD为直角边,画第三个等腰Rt△ADE,…,依此类推,则第2018个等腰直角三角形的斜边长是______.
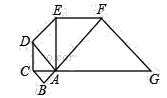
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在△ABC中,AB=AC=4,∠ABC=67.5°,△ABD和△ABC关于AB所在的直线对称,点M为边AC上的一个动点(重合),点M关于AB所在直线的对称点为N,△CMN的面积为S.
(1)求∠CAD的度数;
(2)设CM=x,求S与x的函数表达式,并求x为何值时S的值最大?
(3)S的值最大时,过点C作EC⊥AC交AB的延长线于点E,连接EN(如图2),P为线段EN上一点,Q为平面内一点,当以M,N,P,Q为顶点的四边形是菱形时,请直接写出所有满足条件NP的长.
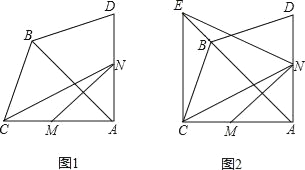
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,一次函数![]() 的图象与反比例函数
的图象与反比例函数![]() 的图象交于点A(
的图象交于点A(![]() ,n)和B.
,n)和B.
(1)求k的值和点B的坐标;
(2)如果P是x轴上一点,且AP=AB,直接写出点P的坐标
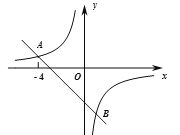
查看答案和解析>>
科目:初中数学 来源: 题型:
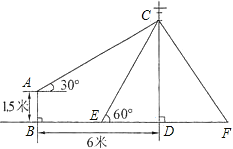
【题目】如图,在电线杆上的C处引拉线CE、CF固定电线杆,拉线CE和地面成60°角,在离电线杆6米的B处安置测角仪,在A处测得电线杆上C处的仰角为30°,已知测角仪高AB为1.5米,求拉线CE的长(结果保留根号).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,点 A(﹣2,0),B(2,0),C(0,2),点 D,点E分别是 AC,BC的中点,将△CDE绕点C逆时针旋转得到△CD′E′,及旋转角为α,连接 AD′,BE′.
(1)如图①,若 0°<α<90°,当 AD′∥CE′时,求α的大小;
(2)如图②,若 90°<α<180°,当点 D′落在线段 BE′上时,求 sin∠CBE′的值;
(3)若直线AD′与直线BE′相交于点P,求点P的横坐标m的取值范围(直接写出结果即可).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某科技公司研发出一款多型号的智能手表,一家代理商出售该公司的![]() 型智能手表,去年销售总额为80000元,今年
型智能手表,去年销售总额为80000元,今年![]() 型智能手表的售价每只比去年降了600元,若今年售出的数量与去年相同的情况下,今年的销售总额将比去年减少
型智能手表的售价每只比去年降了600元,若今年售出的数量与去年相同的情况下,今年的销售总额将比去年减少![]() .
.
(1)求今年![]() 型智能手表每只售价多少元?
型智能手表每只售价多少元?
(2)今年这家代理商准备新进一批![]() 型智能手表和
型智能手表和![]() 型智能手表共100只,它们的进货价与销售价格如下表所示,若
型智能手表共100只,它们的进货价与销售价格如下表所示,若![]() 型智能手表进货量不超过
型智能手表进货量不超过![]() 型智能手表进货量的3倍,所进智能手表可全部售完,请你设计出进货方案,使这批智能手表获利最多,并求出最大利润是多少元?
型智能手表进货量的3倍,所进智能手表可全部售完,请你设计出进货方案,使这批智能手表获利最多,并求出最大利润是多少元?
|
| |
进价 | 1300元/只 | 1500元/只 |
售价 | 今年的售价 | 2300元/只 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com