
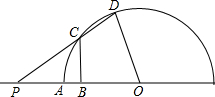
 ��֪��ͼ��ԲO�İ뾶OA=4��P��OA�ӳ�����һ�㣬���߶�OP���е�B�����߽���O�ڵ�C������PC����O�ڵ�D������OD��
��֪��ͼ��ԲO�İ뾶OA=4��P��OA�ӳ�����һ�㣬���߶�OP���е�B�����߽���O�ڵ�C������PC����O�ڵ�D������OD������ ��1���������ô�ֱƽ���ߵ�������CP=CO�����õȱ߶ԵȽǵá�P=��COP����ͬ�����Ե�Բ�Ľ�����á�DOC=��COP��������ǵ����ʺ������ε��ڽǺͶ��������������ó����ۣ�
��2���������ã�1���еĽ��ۣ��������������ε��ж������á�DOC�ס�DPO�����������������ε����ʵ�$\frac{DO}{DP}$=$\frac{DC}{DO}$��������ֵ�ó�CD��
��3���������ĵ㹲Բ�ɵá�PQD+��ACD=180�㣬���ڲ��Ƕ����á�PCA=��PQD���á�PCA�ס�PQD���������������ε�������$\frac{PC}{PQ}=\frac{PA}{PD}$������ɵù�ϵʽ��
��� �⣺��1������OC����ͼ1��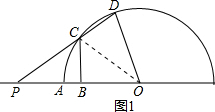
��BC��PO��PB=OB��
��CP=CO��
���P=��COP��
��$\widehat{AC}=\widehat{CD}$��
���DOC=��COP��
�ڡ�COD�У�2��DCO+��DOC=180�㣬
�ߡ�DCO=��P+��COP=2��COP=2��DOC��
��5��DOC=180�㣬
���DOC=36�㣻
��2����$\widehat{AC}=\widehat{CD}$��
���DOC=��COP��
��BC��ֱƽ��OP��
��PC=OC=4��
���P=��POC=��DOC��
���DOC�ס�DPO��
��$\frac{DO}{DP}$=$\frac{DC}{DO}$��
��CD=y����16=��y+4��y����ã�y=2$\sqrt{5}$-2��
��CD�ij�Ϊ2$\sqrt{5}$-2��
��3���ӳ�PO��Բ��Q�㣬����AC����ͼ2��
�ߡ�PQD+��ACD=180�㣬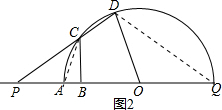
���PCA=��PQD��
�ߡ�P=��P��
���PCA�ס�PQD��
��$\frac{PC}{PQ}=\frac{PA}{PD}$��
��4��4+y��=x��x+8����
��y=$\frac{{x}^{2}+8x-16}{4}$ ��4$\sqrt{2}$-4��x��4����
���� ������Ҫ������Բ�ܽǶ�������ֱƽ���ߵ����ʣ����������ε��ж������ʵȣ������ʵ��ĸ����ߣ��ۺ����ø������ǽ�����Ĺؼ���



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | y=2��x+1��2+3 | B�� | y=-x2+4x+1 | C�� | y=2x2+4x-3 | D�� | y=-2x2-x+5 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��������y=mx2-3mx+2��m��0����x��Ľ���ΪA��x1��0����B��x2��0������x12+x22=17������x1��x2�������ߵĶ���ΪM����P��a��b��Ϊ��������һ���㣮
��������y=mx2-3mx+2��m��0����x��Ľ���ΪA��x1��0����B��x2��0������x12+x22=17������x1��x2�������ߵĶ���ΪM����P��a��b��Ϊ��������һ���㣮�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ������ABCD�У�AB=2AD��APƽ�֡�DAB����AP��DP�ڵ�P������CP����sin��DCP��ֵ��$\frac{\sqrt{10}}{10}$��
��ͼ������ABCD�У�AB=2AD��APƽ�֡�DAB����AP��DP�ڵ�P������CP����sin��DCP��ֵ��$\frac{\sqrt{10}}{10}$���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
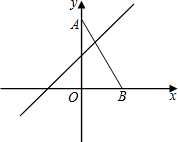 ��֪ƽ��ֱ������ϵ�У�OΪ����ԭ�㣬��A����Ϊ��0��8������B����Ϊ��4��0������E��ֱ��y=x+4�ϵ�һ�����㣬����EAB=��ABO�����E������Ϊ��4��8����-12��-8����
��֪ƽ��ֱ������ϵ�У�OΪ����ԭ�㣬��A����Ϊ��0��8������B����Ϊ��4��0������E��ֱ��y=x+4�ϵ�һ�����㣬����EAB=��ABO�����E������Ϊ��4��8����-12��-8�����鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
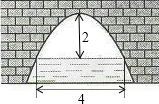 ��ͼ��һ�������Ϊ��������״�Ĺ��ţ���ˮ���4mʱ�����������Ŷ�����ߵ㣩��ˮ��2m����ˮ���½�1mʱ��ˮ��Ŀ���Ϊ��������
��ͼ��һ�������Ϊ��������״�Ĺ��ţ���ˮ���4mʱ�����������Ŷ�����ߵ㣩��ˮ��2m����ˮ���½�1mʱ��ˮ��Ŀ���Ϊ��������| A�� | 3 | B�� | 2$\sqrt{6}$ | C�� | 3$\sqrt{2}$ | D�� | 2 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
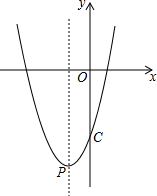 ��֪���κ���y=x2+bx-4��ͼ����y��Ľ���ΪC����x��������Ľ���ΪA����tan��ACO=$\frac{1}{4}$
��֪���κ���y=x2+bx-4��ͼ����y��Ľ���ΪC����x��������Ľ���ΪA����tan��ACO=$\frac{1}{4}$�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
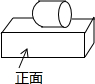 ��ͼ����һ��Բ���ͳ�������϶��ɵļ����壬���ĸ���ͼ�ǣ�������
��ͼ����һ��Բ���ͳ�������϶��ɵļ����壬���ĸ���ͼ�ǣ�������| A�� | 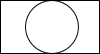 | B�� | 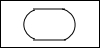 | C�� | 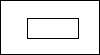 | D�� |  |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com