
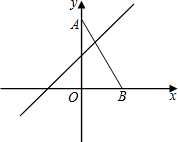 已知平面直角坐标系中,O为坐标原点,点A坐标为(0,8),点B坐标为(4,0),点E是直线y=x+4上的一个动点,若∠EAB=∠ABO,则点E的坐标为(4,8)或(-12,-8).
已知平面直角坐标系中,O为坐标原点,点A坐标为(0,8),点B坐标为(4,0),点E是直线y=x+4上的一个动点,若∠EAB=∠ABO,则点E的坐标为(4,8)或(-12,-8). 分析 分两种情况:当点E在y轴右侧时,由条件可判定AE∥BO,容易求得E点坐标;当点E在y轴左侧时,可设E点坐标为(a,a+4),过AE作直线交x轴于点C,可表示出直线AE的解析式,可表示出C点坐标,再根据勾股定理可表示出AC的长,由条件可得到AC=BC,可得到关于a的方程,可求得E点坐标.
解答 解:
当点E在y轴右侧时,如图1,连接AE,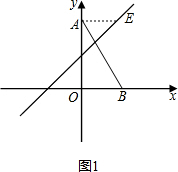
∵∠EAB=∠ABO,
∴AE∥OB,
∵A(0,8),
∴E点纵坐标为8,
又E点在直线y=x+4上,把y=8代入可求得x=4,
∴E点坐标为(4,8);
当点E在y轴左侧时,过A、E作直线交x轴于点C,如图2,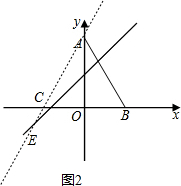
设E点坐标为(a,a+4),设直线AE的解析式为y=kx+b,
把A、E坐标代入可得$\left\{\begin{array}{l}{b=8}\\{ak+b=a+4}\end{array}\right.$,解得$\left\{\begin{array}{l}{k=\frac{a-4}{a}}\\{b=8}\end{array}\right.$,
∴直线AE的解析式为y=$\frac{a-4}{a}$x+8,令y=0可得$\frac{a-4}{a}$x+8=0,解得x=$\frac{8a}{4-a}$,
∴C点坐标为($\frac{8a}{4-a}$,0),
∴AC2=OC2+OA2,即AC2=($\frac{8a}{4-a}$)2+82,
∵B(4,0),
∴BC2=(4-$\frac{8a}{4-a}$)2=($\frac{8a}{4-a}$)2-$\frac{64a}{4-a}$+16,
∵∠EAB=∠ABO,
∴AC=BC,
∴AC2=BC2,即($\frac{8a}{4-a}$)2+82=($\frac{8a}{4-a}$)2-$\frac{64a}{4-a}$+16,
解得a=-12,则a+4=-8,
∴E点坐标为(-12,-8),
综上可知E点坐标为(4,8)或(-12,-8),
故答案为:(4,8)或(-12,-8).
点评 本题主要考查一次函数的综合应用,涉及待定系数法、平行线的判定和性质、等腰三角形的性质、分类讨论思想等知识点.确定出E点的位置,由条件得到AE∥OB或AC=BC是解题的关键.本题难度未大,注意考虑全面即可.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
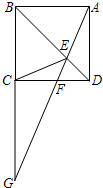 如图,四边形ABCD是矩形,E是BD上的一点,∠BAE=∠BCE,∠AED=∠CED,点G是BC、AE延长线的交点,AG与CD相交于点F,则:①四边形ABCD是正方形;②△CEG∽△FEC;③C是BG的中点;④当AE=2EF时,FG=3EF,正确的有几个( )
如图,四边形ABCD是矩形,E是BD上的一点,∠BAE=∠BCE,∠AED=∠CED,点G是BC、AE延长线的交点,AG与CD相交于点F,则:①四边形ABCD是正方形;②△CEG∽△FEC;③C是BG的中点;④当AE=2EF时,FG=3EF,正确的有几个( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
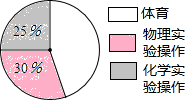 赤峰市对九年级学生的体育、物理实验操作、化学实验操作成绩进行抽样调查,成绩评定为A,B,C,D四个等级.现抽取这三个科目共1000名学生的成绩进行统计分析,其中A,B,C,D分别表示优秀,良好,合格,不合格四个等级.相关数据统计如表及图所示.
赤峰市对九年级学生的体育、物理实验操作、化学实验操作成绩进行抽样调查,成绩评定为A,B,C,D四个等级.现抽取这三个科目共1000名学生的成绩进行统计分析,其中A,B,C,D分别表示优秀,良好,合格,不合格四个等级.相关数据统计如表及图所示.| 等级 人数 科目 | A | B | C | D |
| 物理实验操作 | 120 | 7 | 90 | 20 |
| 化学实验操作 | 90 | 110 | 30 | 20 |
| 体育 | 123 | 140 | 160 | 27 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
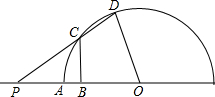 已知如图半圆O的半径OA=4,P是OA延长线上一点,过线段OP的中点B作垂线交⊙O于点C,射线PC交⊙O于点D,联结OD.
已知如图半圆O的半径OA=4,P是OA延长线上一点,过线段OP的中点B作垂线交⊙O于点C,射线PC交⊙O于点D,联结OD.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,已知线段a,b,c.(尺规作图,保留作图痕迹,不写做法)
如图,已知线段a,b,c.(尺规作图,保留作图痕迹,不写做法)查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 4 | B. | 5 | C. | 6 | D. | 7 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
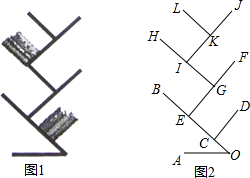 图1是小明利用废弃的钢条焊接成的创意书架,现将其结构简化成图2所示的图形,制作过程为:首先将两根钢条OA和OB焊接成∠AOB=45°,OB=70cm,BC=EF=HG=IJ=60cm,焊接点E、G、I分别为BC、EF、HG的中点,钢条KL、CD的长均为30cm,所有在点C,E,G,I,K焊接处的相邻两根钢条互相垂直.
图1是小明利用废弃的钢条焊接成的创意书架,现将其结构简化成图2所示的图形,制作过程为:首先将两根钢条OA和OB焊接成∠AOB=45°,OB=70cm,BC=EF=HG=IJ=60cm,焊接点E、G、I分别为BC、EF、HG的中点,钢条KL、CD的长均为30cm,所有在点C,E,G,I,K焊接处的相邻两根钢条互相垂直.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com