
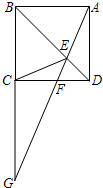
 如图,四边形ABCD是矩形,E是BD上的一点,∠BAE=∠BCE,∠AED=∠CED,点G是BC、AE延长线的交点,AG与CD相交于点F,则:①四边形ABCD是正方形;②△CEG∽△FEC;③C是BG的中点;④当AE=2EF时,FG=3EF,正确的有几个( )
如图,四边形ABCD是矩形,E是BD上的一点,∠BAE=∠BCE,∠AED=∠CED,点G是BC、AE延长线的交点,AG与CD相交于点F,则:①四边形ABCD是正方形;②△CEG∽△FEC;③C是BG的中点;④当AE=2EF时,FG=3EF,正确的有几个( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
分析 ①由∠BAE=∠BCE,∠AED=∠CED,利用三角形外角的性质,即可得∠CBE=∠ABE,又由四边形ABCD是矩形,即可证得△ABD与△BCD是等腰直角三角形,继而证得四边形ABCD是正方形;
②由正方形的性质和条件可证得∠ECD=∠DAE=∠G,可证明△CEG∽△FEC;
③由E点为BD上的任意一点,当E为AC、BD的交点时,则G与C重合,不满足条件;
④由题意易证得△ABE∽△FDE,△ADE∽△GBE,△ADF∽△GCF,由AE=2EF,利用相似三角形的对应边成比例,即可求得FG=3EF.
解答 解:∵∠CED是△BCE的外角,∠AED是△ABE的外角,
∴∠CED=∠CBE+∠BCE,∠AED=∠BAE+∠ABE,
∵∠BAE=∠BCE,∠AED=∠CED,
∴∠CBE=∠ABE,
∵四边形ABCD是矩形,
∴∠ABC=∠BCD=∠BAD=90°,AB=CD,
∴∠CBE=∠ABE=45°,
∴△ABD与△BCD是等腰直角三角形,
∴AB=AD=BC=CD,
∴四边形ABCD是正方形;
故①正确;
∵四边形ABCD为正方形,
∴∠ADE=∠CDE,且∠AED=∠CED,
∴∠DAE=∠DCE,
∵AD∥BC,
∴∠DAE=∠G,
∴∠DCE=∠G,且∠CEF=∠GEC,
∴△CEG∽△FEC,
故②正确;
∵E为BD上任一点,
∴E可为AC、BD的交点,
此时C、G重合,
∴C不是BG的中点,
故③不正确;
∵四边形ABCD是正方形,
∴AB∥CD,AD∥BC,
∴△ABE∽△FDE,△ADE∽△GBE,
∵AE=2EF,
∴BE:DE=AE:EF=2,
∴BG:AD=BE:DE=2,
即BG=2AD,
∵BC=AD,
∴CG=AD,
∵△ADF∽△GCF,
∴FG:AF=CG:AD,
即FG=AF=AE+EF=3EF.
故④正确;
综上可知正确有为①②④.
故选C.
点评 本题主要考查了相似三角形的判定与性质、矩形的性质,正方形的判定与性质、等腰直角三角形的性质以及三角形外角的性质.此题难度适中,注意数形结合思想的应用.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:选择题
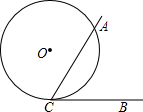 如图,∠ACB=60○,半径为1的⊙O切BC于点C,若将⊙O在直线CB上沿某一方向滚动,当滚动到⊙O与CA也相切时,圆心O移动的水平距离为( )
如图,∠ACB=60○,半径为1的⊙O切BC于点C,若将⊙O在直线CB上沿某一方向滚动,当滚动到⊙O与CA也相切时,圆心O移动的水平距离为( )| A. | $\sqrt{3}$ | B. | $\frac{1}{3}\sqrt{3}$ | C. | π 或$\sqrt{3}$ | D. | $\frac{1}{3}\sqrt{3}$或$\sqrt{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
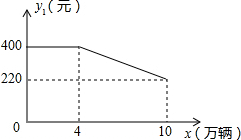 “低碳生活”作为一种健康、环保、安全的生活方式,受到越来越多人的关注.某公司生产的健身自行车在市场上受到普遍欢迎,在国内市场和国外市场畅销,生产的产品可以全部售出,在国内市场每辆的利润y1(元)与销量x(万辆)的关系如图所示;在国外市场每辆的利润y2 (元)与销量x(万量)的关系为:
“低碳生活”作为一种健康、环保、安全的生活方式,受到越来越多人的关注.某公司生产的健身自行车在市场上受到普遍欢迎,在国内市场和国外市场畅销,生产的产品可以全部售出,在国内市场每辆的利润y1(元)与销量x(万辆)的关系如图所示;在国外市场每辆的利润y2 (元)与销量x(万量)的关系为:查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. |  | B. | 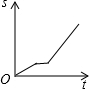 | C. | 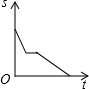 | D. | 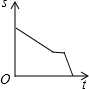 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
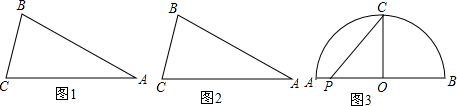
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 设抛物线y=mx2-3mx+2(m≠0)与x轴的交点为A(x1,0),B(x2,0),且x12+x22=17,其中x1<x2,抛物线的顶点为M,点P(a,b)为抛物线上一动点.
设抛物线y=mx2-3mx+2(m≠0)与x轴的交点为A(x1,0),B(x2,0),且x12+x22=17,其中x1<x2,抛物线的顶点为M,点P(a,b)为抛物线上一动点.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
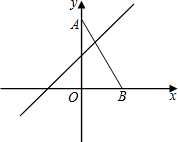 已知平面直角坐标系中,O为坐标原点,点A坐标为(0,8),点B坐标为(4,0),点E是直线y=x+4上的一个动点,若∠EAB=∠ABO,则点E的坐标为(4,8)或(-12,-8).
已知平面直角坐标系中,O为坐标原点,点A坐标为(0,8),点B坐标为(4,0),点E是直线y=x+4上的一个动点,若∠EAB=∠ABO,则点E的坐标为(4,8)或(-12,-8).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com