
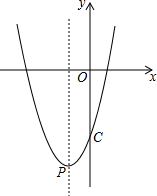
 已知二次函数y=x2+bx-4的图象与y轴的交点为C,与x轴正半轴的交点为A,且tan∠ACO=$\frac{1}{4}$
已知二次函数y=x2+bx-4的图象与y轴的交点为C,与x轴正半轴的交点为A,且tan∠ACO=$\frac{1}{4}$分析 (1)首先根据tan∠ACO=$\frac{1}{4}$,求出OA的值,即可判断出A点的坐标;然后把A点的坐标代入y=x2+bx-4,求出b的值,即可判断出二次函数的解析式.
(2)首先根据Q为抛物线对称轴上的一点,设点Q的坐标为(-$\frac{3}{2}$,n);然后根据∠OQC=∠CQP、∠CQP=∠OCQ,可得∠OQC=∠OCQ,所以OQ=OC,据此求出n的值,进而判断出Q点坐标即可.
(3)根据题意,分3种情况:①当x1≤x2≤-$\frac{3}{2}$时;②当x1≤-$\frac{3}{2}$≤x2时;③当-$\frac{3}{2}$<x1≤x2时;然后根据二次函数的最值的求法,求出满足题意的实数x1、x2(x1<x2),使得当x1≤x≤x2时,y的取值范围为$\frac{12}{{x}_{2}}$≤y≤$\frac{12}{{x}_{1}}$即可.
解答 解:(1)如图1,连接AC,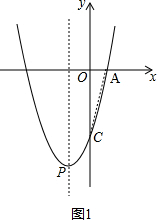 ,
,
∵二次函数y=x2+bx-4的图象与y轴的交点为C,
∴C点的坐标为(0,-4),
∵tan∠ACO=$\frac{1}{4}$,
∴$\frac{OA}{OC}=\frac{1}{4}$,
又∵OC=4,
∴OA=1,
∴A点的坐标为(1,0),
把A(1,0)代入y=x2+bx-4,
可得0=1+b-4,
解得b=3,
∴二次函数的解析式是:y=x2+3x-4.
(2)如图2,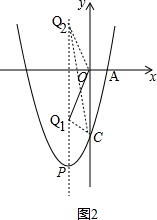 ,
,
∵y=x2+3x-4,
∴抛物线的对称轴是:x=-$\frac{3}{2}$,
∵Q为抛物线对称轴上的一点,
∴设点Q的坐标为(-$\frac{3}{2}$,n),
∵抛物线的对称轴平行于y轴,
∴∠CQP=∠OCQ,
又∵∠OQC=∠CQP,
∴∠OQC=∠OCQ,
∴OQ=OC,
∴$\sqrt{{(-\frac{3}{2})}^{2}{+n}^{2}}=4$,
∴${n}^{2}+\frac{9}{4}=16$,
解得n=±$\frac{\sqrt{55}}{2}$,
∴Q点坐标是(-$\frac{3}{2}$,$\frac{\sqrt{55}}{2}$)或(-$\frac{3}{2}$,-$\frac{\sqrt{55}}{2}$).
(3)①当x1≤x2≤-$\frac{3}{2}$时,二次函数y=x2+3x-4单调递减,
∵y的取值范围为$\frac{12}{{x}_{2}}$≤y≤$\frac{12}{{x}_{1}}$,
∴$\left\{\begin{array}{l}{{{x}_{1}}^{2}+{3x}_{1}-4=\frac{12}{{x}_{1}}}\\{{{x}_{2}}^{2}+{3x}_{2}-4=\frac{12}{{x}_{2}}}\end{array}\right.$
由${{x}_{1}}^{2}$+3x1-4=$\frac{12}{{x}_{1}}$,
解得x1=-3,-2,2,
由${{x}_{2}}^{2}$+3x2-4=$\frac{12}{{x}_{2}}$,
解得x2=-3,-2,2,
∵x1≤x2≤-$\frac{3}{2}$,
∴$\left\{\begin{array}{l}{{x}_{1}=-3}\\{{x}_{2}=-2}\end{array}\right.$
②当x1≤-$\frac{3}{2}$≤x2时,
Ⅰ、当-$\frac{3}{2}{-x}_{1}{≥x}_{2}-(-\frac{3}{2})$时,
可得x1+x2≤-3,
∵y的取值范围为$\frac{12}{{x}_{2}}$≤y≤$\frac{12}{{x}_{1}}$,
∴$\left\{\begin{array}{l}{\frac{4×1×(-4){-3}^{2}}{4×1}=\frac{12}{{x}_{2}}…(1)}\\{{{x}_{1}}^{2}+{3x}_{1}-4=\frac{12}{{x}_{1}}…(2)}\end{array}\right.$
由(1),可得${x}_{2}=-\frac{48}{25}$,
由(2),可得x1=-3,-2,2,
∵x1≤-$\frac{3}{2}$<x2,$-\frac{3}{2}>-\frac{48}{25}$,
∴没有满足题意的x1、x2.
Ⅱ、当-$\frac{3}{2}{-x}_{1}{<x}_{2}-(-\frac{3}{2})$时,
可得x1+x2>-3,
∵y的取值范围为$\frac{12}{{x}_{2}}$≤y≤$\frac{12}{{x}_{1}}$,
∴$\left\{\begin{array}{l}{\frac{4×1×(-4){-3}^{2}}{4×1}=\frac{12}{{x}_{2}}}\\{{{x}_{2}}^{2}+{3x}_{2}-4=\frac{12}{{x}_{1}}}\end{array}\right.$
解得$\left\{\begin{array}{l}{{x}_{1}=-\frac{1875}{949}}\\{{x}_{2}=-\frac{48}{25}}\end{array}\right.$
∵x1+x2=$-\frac{1875}{949}-\frac{48}{25}$≈-1.98-1.92=-3.9<-3,
∴没有满足题意的x1、x2.
③当-$\frac{3}{2}$<x1≤x2时,
二次函数y=x2+3x-4单调递增,
∵y的取值范围为$\frac{12}{{x}_{2}}$≤y≤$\frac{12}{{x}_{1}}$,
∴$\left\{\begin{array}{l}{{{x}_{1}}^{2}+{3x}_{1}-4=\frac{12}{{x}_{2}}…(1)}\\{{{x}_{2}}^{2}+{3x}_{2}-4=\frac{12}{{x}_{1}}…(2)}\end{array}\right.$
(1)×x2-(2)×x1,可得
(x1-x2)(x1x2+4)=0,
∵x1-x2≠0,
∴x1x2+4=0,
∴${x}_{2}=-\frac{4}{{x}_{1}}$…(1),
把(3)代入(1),可得
${x}_{1}=-3±\sqrt{13}$,
∵${x}_{1}>-\frac{3}{2}$,
∴${x}_{1}=\sqrt{13}-3$,
∴${x}_{2}=\frac{-4}{{x}_{1}}=-\sqrt{13}-3$,
∵$-\sqrt{13}-3<-\frac{3}{2}$,
∴没有满足题意的x1、x2.
综上,可得
x1=-3,x2=-2时,当x1≤x≤x2时,y的取值范围为$\frac{12}{{x}_{2}}$≤y≤$\frac{12}{{x}_{1}}$.
点评 (1)此题主要考查了二次函数综合题,考查了分析推理能力,考查了分类讨论思想的应用,考查了从已知函数图象中获取信息,并能利用获取的信息解答相应的问题的能力.
(2)此题还考查了待定系数法求二次函数的解析式的方法,以及二次函数的最值的求法,要熟练掌握.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
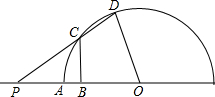 已知如图半圆O的半径OA=4,P是OA延长线上一点,过线段OP的中点B作垂线交⊙O于点C,射线PC交⊙O于点D,联结OD.
已知如图半圆O的半径OA=4,P是OA延长线上一点,过线段OP的中点B作垂线交⊙O于点C,射线PC交⊙O于点D,联结OD.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,已知线段a,b,c.(尺规作图,保留作图痕迹,不写做法)
如图,已知线段a,b,c.(尺规作图,保留作图痕迹,不写做法)查看答案和解析>>
科目:初中数学 来源: 题型:填空题
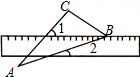 将一把有刻度的直尺摆放在含30°角的三角板(∠A=30°,∠C=90°)上,其中顶点B在直尺的一边上,已知∠1=55°,则∠2=25度.
将一把有刻度的直尺摆放在含30°角的三角板(∠A=30°,∠C=90°)上,其中顶点B在直尺的一边上,已知∠1=55°,则∠2=25度.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 4 | B. | 5 | C. | 6 | D. | 7 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
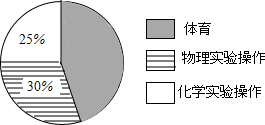 我市准备对九年级学生的体育、物理实验操作、化学实验操作成绩实行等级制改革,成绩评定为A、B、C、D四个等级,现抽取这三种成绩共1000份数据进行统计分析,其中A、B、C、D分别表示优秀、良好、合格、不合格四个等级,相关数据统计如下图表所示.
我市准备对九年级学生的体育、物理实验操作、化学实验操作成绩实行等级制改革,成绩评定为A、B、C、D四个等级,现抽取这三种成绩共1000份数据进行统计分析,其中A、B、C、D分别表示优秀、良好、合格、不合格四个等级,相关数据统计如下图表所示.| 等级 人数 项目 | A | B | C | D |
| 物理实验操作 | 120 | 70 | 90 | 20 |
| 化学实验操作 | 90 | 110 | 30 | 20 |
| 体育 | 123 | 140 | 160 | 27 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com