
分析 (1)可得抛物线y=ax2-2ax+4的对称轴是x=1,根据AB=6,由对称性可得点A(-2,0),根据待定系数法可求抛物线的解析式为y=-$\frac{1}{2}$x2+x+4;
(2)如图1,连接CE,延长CQ交x轴于点G,可证四边形CGBE是平行四边形,过点Q作QT⊥OC于点T,在Rt△QCT中,设QT=m,则CT=2m,由OQ平分∠COB,可得QT=OT=m,OC=3m=4,解得m=$\frac{4}{3}$,从而得到点Q坐标($\frac{4}{3}$,$\frac{4}{3}$);
(3)根据待定系数法可得直线BF解析式为y=-$\frac{1}{2}$x+2,将点F(x,-$\frac{1}{2}$x+2)代入抛物线的解析式可得-$\frac{1}{2}$x+2=-$\frac{1}{2}$x2+x+4,可得点F(-1,$\frac{5}{2}$),由对称性FH=KH=2,得点K(3,$\frac{5}{2}$),得到点D(1,$\frac{9}{2}$),DH=$\frac{9}{2}$-$\frac{5}{2}$=2,设点P坐标为(m,-$\frac{1}{2}$m2+m+4),过点P作PS⊥DH于点S,PN⊥FK于点N,如图2,由三角函数得到MH=m-1=PS=HN,连结DF,DK延长DP交FK延长线于点R,可证△DFG≌△DKR,得到FG=KR=2(m-1),在Rt△PNR中tan∠R=$\frac{PN}{NR}$=$\frac{-\frac{1}{2}(m-3)(m+1)}{m+1}$=$\frac{1}{2}$(3-m),在Rt△DHR中tan∠R=$\frac{DH}{HR}$=$\frac{2}{2m}$=$\frac{1}{m}$,可得$\frac{1}{2}$(3-m)=$\frac{1}{m}$,得到点P坐标(2,4),进一步得到S=$\frac{8}{3}$.
解答 解:(1)抛物线y=ax2-2ax+4的对称轴是x=1,
∵AB=6,
∴由对称性可得点A(-2,0),将A(-2,0)代入解析式可得4a+4a+4=0,解得a=-$\frac{1}{2}$,
∴抛物线的解析式为y=-$\frac{1}{2}$x2+x+4;
(2)如图1,连接CE,延长CQ交x轴于点G,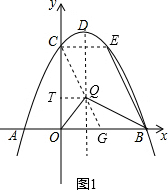 点C(0,4),对称轴是x=1,由对称性可得点E(2,4),
点C(0,4),对称轴是x=1,由对称性可得点E(2,4),
∴CE=2,CE∥x轴,
∵CG∥BE,
∴四边形CGBE是平行四边形,
∴BG=2,
∴OG=2,
∴tan∠OCG=$\frac{1}{2}$,
过点Q作QT⊥OC于点T,在Rt△QCT中,设QT=m,则CT=2m,
∵OQ平分∠COB,
∴∠QOC=45°,
∴QT=OT=m,
∴OC=3m=4,
∴m=$\frac{4}{3}$,
∴点Q坐标($\frac{4}{3}$,$\frac{4}{3}$);
(3)设直线BF解析式为y=kx+b过点B(4,0)、Q($\frac{4}{3}$,$\frac{4}{3}$),可得解析式为y=-$\frac{1}{2}$x+2,
将点F(x,-$\frac{1}{2}$x+2)代入抛物线的解析式可得-$\frac{1}{2}$x+2=-$\frac{1}{2}$x2+x+4,
解得x1=4(舍去),x2=-1,
∴点F(-1,$\frac{5}{2}$),
由对称性FH=KH=2,得点K(3,$\frac{5}{2}$),
当x=1时,y=-$\frac{1}{2}$×12+1+4=$\frac{9}{2}$,
∴点D(1,$\frac{9}{2}$),
∴DH=$\frac{9}{2}$-$\frac{5}{2}$=2,
设点P坐标为(m,-$\frac{1}{2}$m2+m+4),过点P作PS⊥DH于点S,PN⊥FK于点N,如图2,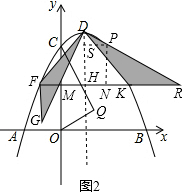 ∴HN=PS=m-1,DS=$\frac{9}{2}$+$\frac{1}{2}$m2-m-4=$\frac{1}{2}$(m-1)2,
∴HN=PS=m-1,DS=$\frac{9}{2}$+$\frac{1}{2}$m2-m-4=$\frac{1}{2}$(m-1)2,
tan∠DPS=$\frac{1}{2}$(m-1),∠PDM=90°,
∴∠MDH=∠DPS,
∴tan∠MDH=tan∠DPS,
$\frac{MH}{DH}$=$\frac{1}{2}$(m-1),
∴MH=m-1=PS=HN,
∵FG=2MH=2(m-1),
连结DF,DK延长DP交FK延长线于点R,
由FH=KH=DH可得∠FDK=90°,∠DFK=∠DKF=45°,∠DFG=∠DKR=135°,
∴∠MDF=∠KDR,
∴△DFG≌△DKR,
∴FG=KR=2(m-1),
PN=-$\frac{1}{2}$m2+m+4-$\frac{5}{2}$=-$\frac{1}{2}$m2+m+$\frac{3}{2}$=-$\frac{1}{2}$(m-3)(m+1),
NR=NK+KR=3-m+2(m-1)=m+1,
HR=KR+HK=2+(2m-1)=2m,
在Rt△PNR中tan∠R=$\frac{PN}{NR}$=$\frac{-\frac{1}{2}(m-3)(m+1)}{m+1}$=$\frac{1}{2}$(3-m),
在Rt△DHR中tan∠R=$\frac{DH}{HR}$=$\frac{2}{2m}$=$\frac{1}{m}$,
∴$\frac{1}{2}$(3-m)=$\frac{1}{m}$,
解得m1=1(舍去),m2=2,
∴点P坐标(2,4),
∴S=$\frac{8}{3}$.
点评 本题主要考查了二次函数综合题,直线上点的坐标特征、用待定系数法求抛物线的解析式、全等三角形的判定与性质、勾股定理、解一元二次方程等知识,对运算能力的要求比较高,有一定的难度;将QT及CT用t的代数式表示则是解决第(2)小题的关键,证到FG=KR则是解决第(3)小题的关键.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | y=2(x+1)2+3 | B. | y=-x2+4x+1 | C. | y=2x2+4x-3 | D. | y=-2x2-x+5 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
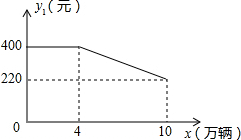 “低碳生活”作为一种健康、环保、安全的生活方式,受到越来越多人的关注.某公司生产的健身自行车在市场上受到普遍欢迎,在国内市场和国外市场畅销,生产的产品可以全部售出,在国内市场每辆的利润y1(元)与销量x(万辆)的关系如图所示;在国外市场每辆的利润y2 (元)与销量x(万量)的关系为:
“低碳生活”作为一种健康、环保、安全的生活方式,受到越来越多人的关注.某公司生产的健身自行车在市场上受到普遍欢迎,在国内市场和国外市场畅销,生产的产品可以全部售出,在国内市场每辆的利润y1(元)与销量x(万辆)的关系如图所示;在国外市场每辆的利润y2 (元)与销量x(万量)的关系为:查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 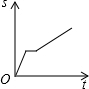 | B. | 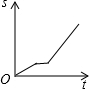 | C. | 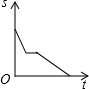 | D. | 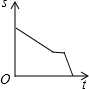 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 设抛物线y=mx2-3mx+2(m≠0)与x轴的交点为A(x1,0),B(x2,0),且x12+x22=17,其中x1<x2,抛物线的顶点为M,点P(a,b)为抛物线上一动点.
设抛物线y=mx2-3mx+2(m≠0)与x轴的交点为A(x1,0),B(x2,0),且x12+x22=17,其中x1<x2,抛物线的顶点为M,点P(a,b)为抛物线上一动点.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
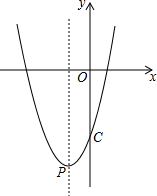 已知二次函数y=x2+bx-4的图象与y轴的交点为C,与x轴正半轴的交点为A,且tan∠ACO=$\frac{1}{4}$
已知二次函数y=x2+bx-4的图象与y轴的交点为C,与x轴正半轴的交点为A,且tan∠ACO=$\frac{1}{4}$查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com