
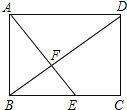
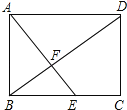
【题目】如图,四边形ABCD是矩形,点E在BC边上,AE与BD交于点F,∠BAE=∠ADB.
(1)图中与△ABF相似的三角形(不包括△ABF本身)共有_____个.
(2)若BE=2,AD=5.求:AB的长.
【答案】(1)5;(2)AB=![]() .
.
【解析】
(1)证明AE⊥BD,即可解决问题.
(2)证明△ABD∽△EBA,得到![]() ,而AD=5,BE=2,求出AB的长度,即可解决问题.
,而AD=5,BE=2,求出AB的长度,即可解决问题.
解:(1)∵四边形ABCD为矩形,
∴∠BAD=∠ABE=∠BCD=90°,而∠BAE=∠ADB,
∴∠BAF+∠ABF=∠ABF+∠ADB=90°,
∴AE⊥BD;
∴△ABE、△BEF、△ABD、△AFD、△BCD均与△ABF相似,
故答案为5.
(2)由(1)知:AE⊥BD,∠ABE=90°,
∴∠ABF+∠EBF=∠EBF+∠FEB,
∴∠ABD=∠AEB,而∠BAD=∠ABE,
∴△ABD∽△EBA,
∴![]() ,而AD=5,BE=2,
,而AD=5,BE=2,
∴AB=![]() .
.


科目:初中数学 来源: 题型:
【题目】已知二次函数![]() ,
,
(1)该二次函数图象与x轴的交点坐标是______________;
(2)将![]() 化成
化成![]() 的形式_____________________,并写出顶点坐标______________.
的形式_____________________,并写出顶点坐标______________.
(3)在坐标轴中画出此抛物线的大致图象;
(4)写出不等式![]() 的解集___________________;
的解集___________________;
(5)当![]() 时,直接写出y的取值范围_________________.
时,直接写出y的取值范围_________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市射击队打算从君君、标标两名运动员中选拔一人参加省射击比赛,射击队对两人的射击技能进行了测评.在相同的条件下,两人各打靶5次,成绩统计如下:
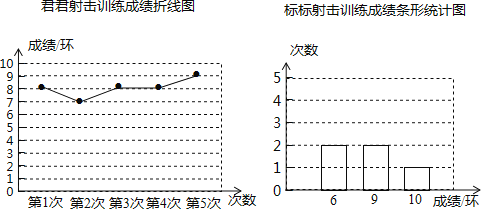
(1)填写下表:
平均数(环) | 中位数(环) | 方差(环2) | |
君君 |
| 8 | 0.4 |
标标 | 8 |
|
|
(2)根据以上信息,若选派一名队员参赛,你认为应选哪名队员,并说明理由.
(3)如果标标再射击1次,命中8环,那么他射击成绩的方差会 .(填“变大”“变小”或“不变”)
查看答案和解析>>
科目:初中数学 来源: 题型:
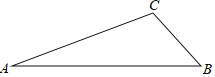
【题目】如图,在△ABC纸板中,AC=4,BC=2,AB=5,P是AC上一点,过点P沿直线剪下一个与△ABC相似的小三角形纸板,如果有4种不同的剪法,那么AP长的取值范围是__.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:若关于x的一元二次方程ax2+bx+c=0(a≠0)的两个实数根为x1,x2(x1<x2),分别以x1,x2为横坐标和纵坐标得到点M(x1,x2),则称点M为该一元二次方程的衍生点.
(1)若方程为x2-2x=0,写出该方程的衍生点M的坐标.
(2)若关于x的一元二次方程x2-(2m+1)x+2m=0(m<0)的衍生点为M,过点M向x轴和y轴作垂线,两条垂线与坐标轴恰好围成一个正方形,求m的值.
(3)是否存在b,c,使得不论k(k≠0)为何值,关于x的方程x2+bx+c=0的衍生点M始终在直线y=kx-2(k-2)的图象上,若有请直接写出b,c的值,若没有说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
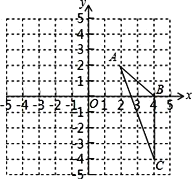
【题目】如图,在平面直角坐标系中,△ABC三个顶点分别是A(2,2),B(4,0),C(4,﹣4)
(1)以点O为位似中心,将△ABC缩小为原来的![]() ,得到△A2B2C2,请在y轴右侧画出△A2B2C2
,得到△A2B2C2,请在y轴右侧画出△A2B2C2
(2)求出∠A2C2B2的正弦值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】校园空地上有一面墙,长度为20m,用长为32m的篱笆和这面墙围成一个矩形花圃,如图所示.
(1)能围成面积是126m2的矩形花圃吗?若能,请举例说明;若不能,请说明理由.
(2)若篱笆再增加4m,围成的矩形花圃面积能达到170m2吗?请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了满足师生的阅读需求,某校图书馆的藏书从2016年底到2018年底两年内由5万册增加到7.2万册.
(1)求这两年藏书的年均增长率;
(2)经统计知:中外古典名著的册数在2016年底仅占当时藏书总量的5.6%,在这两年新增加的图书中,中外古典名著所占的百分率恰好等于这两年藏书的年均增长率,那么到2018年底中外古典名著的册数占藏书总量的百分之几?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com