
����Ŀ����ʦ��ͬѧ�Dz�����һ������ƽ������һ�㣬ʹ�õ㵽���������ε���������ľ�����ȡ��ij߹���ͼ����
������С��ͬѧ��Ƶij߹���ͼ���̣�
��֪����ͼ��![]() �У�
��![]() ��
��
������һ��![]() ��ʹ��
��ʹ��![]() .
.
������
����![]() ��ƽ����
��ƽ����![]() ��
��![]() �ڵ�
�ڵ�![]() ��
��
������![]() �Ĵ�ֱƽ����
�Ĵ�ֱƽ����![]() ��
��![]() ��
��![]() �ཻ�ڵ�
�ཻ�ڵ�![]() ��
��
������![]() ��
��
���ԣ���![]() �����������ĵ�.
�����������ĵ�.
����С��ͬѧ��Ƶij߹���ͼ���̣�
��1��ʹ��ֱ�ߺ�Բ�棬��ȫͼ�Σ�������ͼ�ۼ���
��2����������֤��.
֤������![]() ��
��![]() ƽ��
ƽ��![]() ��
��![]() �ڵ�
�ڵ�![]() ��
��
��![]() ��
��![]() �Ĵ�ֱƽ���ߣ��� �������������ݣ�
�Ĵ�ֱƽ���ߣ��� �������������ݣ�
��![]() .
.
��![]() ��ֱƽ��
��ֱƽ��![]() ����
����![]() �ڵ�
�ڵ�![]() ��
��
��![]() ���� �������������ݣ�
���� �������������ݣ�
��![]() .
.
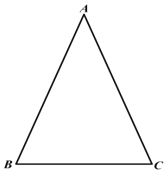
���𰸡���1������������2�����������ε����ߺ�һ �߶δ�ֱƽ�����ϵĵ㵽�߶����˵�ľ������.
��������
��1�����û�����ͼ����ƽ����AD��AB�Ĵ�ֱƽ���ߣ������ཻ��P�㣻
��2�����ݵ��������ε����ʵõ�PB=PC���ٸ����߶δ�ֱƽ�����ϵĵ㵽�߶����˵ľ�����ȵõ�PA=PC���Ӷ��õ�PA=PB=PC��
��1����ͼ��AD����PΪ����

��2��֤������![]() ��
��![]() ƽ��
ƽ��![]() ��
��![]() �ڵ�
�ڵ�![]() ��
��
��![]() ��
��![]() �Ĵ�ֱƽ���ߣ��� ���������ε����ߺ�һ �������������ݣ�
�Ĵ�ֱƽ���ߣ��� ���������ε����ߺ�һ �������������ݣ�
��![]() .
.
��![]() ��ֱƽ��
��ֱƽ��![]() ����
����![]() �ڵ�
�ڵ�![]() ��
��
��![]() ���� �߶δ�ֱƽ�����ϵĵ㵽�߶����˵�ľ������ �������������ݣ�
���� �߶δ�ֱƽ�����ϵĵ㵽�߶����˵�ľ������ �������������ݣ�
��![]() .
.



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
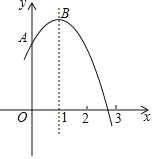
����Ŀ����ͼ��������y����x2+2x+2��y���ڵ�A����x���һ��������2��3֮�䣬����ΪB������˵����������ȷ�жϵ�����ǣ�������
����������ֱ��y��3����ֻ��һ�����㣻
������M����2,y1����N��1,y2����P��2,y3���ڸú���ͼ���ϣ���y1��y2��y3��
�۽��������������������¾�ƽ��2����λ�����������߽���ʽΪy����x+1��2+1��
����x������һ��D��ʹAD+BD�ĺ���С������СֵΪ![]() ��
��
A.�٢ڢ�B.�٢ڢ�C.�٢ۢ�D.�ڢۢ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����9�֣�Ϊ���� �������Ļ�����ij��λ��չ���������Ļ�֮�����ݽ��������ڰ���1λŮѡ�ֺ�3λ��ѡ�ֵij���˳��ʱ�����������ǩ��ʽ��
��1����ֱ��д����һλ������Ůѡ�ֵĸ��ʣ�
��2�������û���״ͼ���б��ķ�����ʾ��һ����λ����ѡ�ֵ����еȿ��ܽ������������Ƕ�����ѡ�ֵĸ��ʣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���������ң���1��ͼ��1���������Ρ�6�������κ�6���ȱ���������ɣ���2��ͼ��2���������Ρ�11�������κ�10���ȱ���������ɣ���3��ͼ��3���������Ρ�16�������κ�14���ȱ���������ɣ��������մ˹��ɣ���n��ͼ�������κ͵ȱ������εĸ���֮��Ϊ������������

A.9nB.6nC.9n��3D.6n+3
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
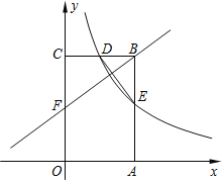
����Ŀ����ͼ������OABC�Ķ���A��C�ֱ���x���y���ϣ���B������Ϊ![]() ��˫����
��˫����![]() ��ͼ��BC���е�D������AB���ڵ�E������DE��
��ͼ��BC���е�D������AB���ڵ�E������DE��
��1����k��ֵ����E�����ꣻ
��2������F��OC����һ�㣬����FBC�ס�DEB����ֱ��FB�Ľ���ʽ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����MAN=30����������AN��ȡһ��B��ʹAB=4 cm������B��BC��AM�ڵ�C����DΪ��AB�ϵĶ��㣨��D�����A����B�غϣ�������CD������D��ED��CD��ֱ��AC�ڵ�E���ڵ�D�ɵ�A����B�˶������У���AD=x cm��AE=y cm��
��1��ȡָ������ͼ�������������Ԥ��������ͨ����ͼȷ��AD=2 cmʱ����E��λ�ã�����AE�ij��ȣ�
���������⣬�ڴ���ϲ�ȫͼ�Σ�
���ѱ���������ͨ��ȡ�㡢��ͼ���������õ���x��y�ļ����Ӧֵ�������
x/cm | �� |
| 1 |
| 2 |
| 3 |
| �� |
y cm | �� | 0.4 | 0.8 | 1.0 | m | 1.0 | 0 | 4.0 | �� |
��m=______���������һλС������
��2���������ƽ��ֱ������ϵxOy�У�����Բ�ȫ��ı��и��Զ�ӦֵΪ����ĵ㣬�����ú�����ͼ��
��3����ϻ����ĺ���ͼ������⣺��AE=![]() ADʱ��AD�ij���ԼΪ______cm��
ADʱ��AD�ij���ԼΪ______cm��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
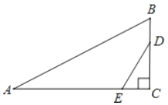
����Ŀ����Rt��ABC�У���C=90����AC=8��BC=6����D��E�ֱ���BC��AC�ϣ���BD=CE�����C����DE�ĶԳƵ�ΪF����DF��AB����BD�ij�Ϊ__________��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����壺�������ε�һ���е���Աߵ����˵���߶ΰ����ֳ����������Σ�����������������������ƣ���ô������������Ϊ���������Σ�
(1)�ж����������������⣬���Ǽ����⣿
��������������������
����һ���ڽ�Ϊ60�������������������Σ�
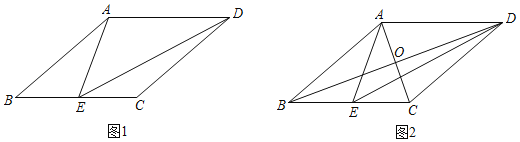
����ͼ1��������ABCD�����������Σ���ABC=��(0��������90��)��EΪBC�е㣬���ڡ�ABE����AED����EDC�У����Ƶ�������ֻ�С�ABE���AED��
(2)��ͼ2������ABCD�����������Σ���ABC����ǣ��߳�Ϊ4��EΪBC�е㣮
����AE��DE�ij���
��AC��BD���ڵ�O����tan��DBC��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
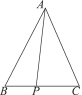
����Ŀ����ͼ����ABC����AB��AC����BAC��50�㣬P��BC����һ��������ABP�Ƶ�A��ʱ����ת50�㣬��P��ת��Ķ�Ӧ��Ϊ��P��.
(1)������ת��������Σ�
(2)����PP�䣬����BAP��20�㣬���PP��C�Ķ�����
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com