
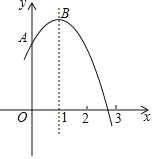
【题目】如图,抛物线y=﹣x2+2x+2交y轴于点A,与x轴的一个交点在2和3之间,顶点为B.下列说法:其中正确判断的序号是( )
①抛物线与直线y=3有且只有一个交点;
②若点M(﹣2,y1),N(1,y2),P(2,y3)在该函数图象上,则y1<y2<y3;
③将该抛物线先向左,再向下均平移2个单位,所得抛物线解析式为y=(x+1)2+1;
④在x轴上找一点D,使AD+BD的和最小,则最小值为![]() .
.
A.①②④B.①②③C.①③④D.②③④
【答案】C
【解析】
根据抛物线的性质和平移,以及一动点到两定点距离之和最小问题的处理方法,对选项进行逐一分析即可.
①抛物线的顶点![]() ,则抛物线与直线y=3有且只有一个交点,正确,符合题意;
,则抛物线与直线y=3有且只有一个交点,正确,符合题意;
②抛物线x轴的一个交点在2和3之间,
则抛物线与x轴的另外一个交点坐标在x=0或x=﹣1之间,
则点N是抛物线的顶点为最大,点P在x轴上方,点M在x轴的下放,
故y1<y3<y2,故错误,不符合题意;
③y=﹣x2+2x+2=﹣(x+1)2+3,将该抛物线先向左,再向下均平移2个单位,
所得抛物线解析式为y=(x+1)2+1,正确,符合题意;
④点A关于x轴的对称点![]() ,连接A′B交x轴于点D,
,连接A′B交x轴于点D,
则点D为所求,距离最小值为BD′=![]() =
=![]() ,
,
正确,符合题意;
故选:C.


科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,直线y=﹣3x+3与x轴、y轴分别交于A、B两点,以AB为边在第一象限作正方形ABCD,点D在双曲线![]() (k≠0)上.将正方形沿x轴负方向平移a个单位长度后,点C恰好落在该双曲线上,则a的值是
(k≠0)上.将正方形沿x轴负方向平移a个单位长度后,点C恰好落在该双曲线上,则a的值是

A.1B.2C.3D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙、丙,丁四个人做“击鼓传花”游戏,游戏规则是:第一次由甲将花随机传给乙、丙、丁三人中的某一人中的某一人,以后的每一次传花都是由接到花的人随机传给其他三人中的某一人.
(1)甲第一次传花时,恰好传给乙的概率是 ;
(2)求经过两次传花,花恰好回到甲手中的概率;
(3)经过三次传花,花落在丙手上的概率记作P1,落在丁手上的概率记作P2,则P1 P2(填“>”、“<”或者“=”)
查看答案和解析>>
科目:初中数学 来源: 题型:
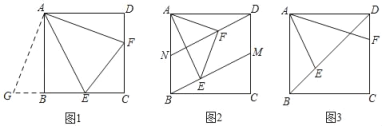
【题目】已知:正方形ABCD,∠EAF=45°.
(1)如图,当点E、F分别在边BC、CD上,连接EF,求证:EF=BE+DF;
童威同学是这样思考的,请你和他一起完成如下解答:证明:将△ADF绕点A顺时针旋转90°,得△ABG,所以△ADF≌△ABG.
(2)如图,点M、N分别在边AB、CD上,且BN=DM.当点E、F分别在BM、DN上,连接EF,探究三条线段EF、BE、DF之间满足的数量关系,并证明你的结论.
(3)如图,当点E、F分别在对角线BD、边CD上.若FC=2,则BE的长为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】图1是一台实物投影仪,图2是它的示意图,折线O﹣A﹣B﹣C表示支架,支架的一部分O﹣A﹣B是固定的,另一部分BC是可旋转的,线段CD表示投影探头,OM表示水平桌面,AO⊥OM,垂足为点O,且AO=7cm,∠BAO=160°,BC∥OM,CD=8cm.
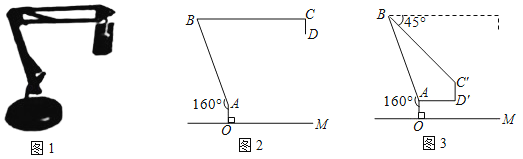
将图2中的BC绕点B向下旋转45°,使得BCD落在BC′D′的位置(如图3所示),此时C′D′⊥OM,AD′∥OM,AD′=16cm,求点B到水平桌面OM的距离,(参考数据:sin70°≈0.94,cos70°≈0.34,cot70°≈0.36,结果精确到1cm)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,一透明的敞口正方体容器ABCD﹣A'B'C'D'装有一些液体,棱AB始终在水平桌面上,液面刚好过棱CD,并与棱BB'交于点Q.此时液体的形状为直三棱柱,其三视图及尺寸见下图所示请解决下列问题:
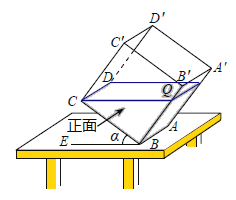
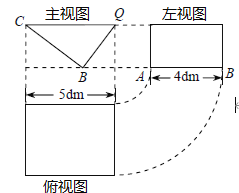
(1)CQ与BE的位置关系是 ,BQ的长是 dm:
(2)求液体的体积;(提示:直棱柱体积=底面积×高)
(3)若容器底部的倾斜角∠CBE=α,求α的度数.(参考数据:sin49°=cos41°=![]() ,tan37°=
,tan37°=![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
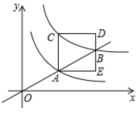
【题目】如图,过原点的直线与反比例函数y=![]() (x>0)、反比例函数y=
(x>0)、反比例函数y=![]() (x>0)的图象分别交于A、B两点,过点A作y轴的平行线交反比例函数y=
(x>0)的图象分别交于A、B两点,过点A作y轴的平行线交反比例函数y=![]() (x>0)的图象于C点,以AC为边在直线AC的右侧作正方形ACDE,点B恰好在边DE上,则正方形ACDE的面积为______.
(x>0)的图象于C点,以AC为边在直线AC的右侧作正方形ACDE,点B恰好在边DE上,则正方形ACDE的面积为______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,点E、F分别在BC、CD上,△AEF是等边三角形,连接AC交EF于点G,下列结论:①![]() ;②AG=
;②AG=![]() GC;③BE+DF=EF;④
GC;③BE+DF=EF;④![]() .其中正确的是( )
.其中正确的是( )

A.①②③B.①③④C.①②④D.①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
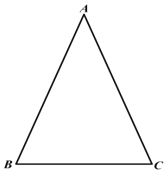
【题目】老师给同学们布置了一个“在平面内找一点,使该点到等腰三角形的三个顶点的距离相等”的尺规作图任务:
下面是小聪同学设计的尺规作图过程:
已知:如图,![]() 中,
中,![]() ,
,
求作:一点![]() ,使得
,使得![]() .
.
作法:
①作![]() 的平分线
的平分线![]() 交
交![]() 于点
于点![]() ;
;
②作边![]() 的垂直平分线
的垂直平分线![]() ,
,![]() 与
与![]() 相交于点
相交于点![]() ;
;
③连接![]() ,
,
所以,点![]() 就是所求作的点.
就是所求作的点.
根据小聪同学设计的尺规作图过程,
(1)使用直尺和圆规,补全图形(保留作图痕迹)
(2)完成下面的证明.
证明:∵![]() ,
,![]() 平分
平分![]() 交
交![]() 于点
于点![]() ,
,
∴![]() 是
是![]() 的垂直平分线;( )(填推理依据)
的垂直平分线;( )(填推理依据)
∴![]() .
.
∵![]() 垂直平分
垂直平分![]() ,交
,交![]() 于点
于点![]() ,
,
∴![]() ;( )(填推理依据)
;( )(填推理依据)
∴![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com