
【题目】A(0,4)是直角坐标系y轴上一点,P是x轴上一动点,从原点O出发,沿正半轴运动,速度为每秒1个单位长度,以P为直角顶点在第一象限内作等腰Rt△APB.设P点的运动时间为t秒.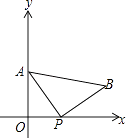
(1)若AB∥x轴,求t的值;
(2)设点B的坐标为(x,y),试求y关于x的函数表达式;
(3)当t=3时,平面直角坐标系内有一点M(3,a),请直接写出使△APM为等腰三角形的点M的坐标.
【答案】
(1)
解:过点B作BC⊥x轴于点C,如图1所示.
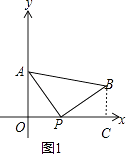
∵AO⊥x轴,BC⊥x轴,且AB∥x轴,
∴四边形ABCO为长方形,
∴AO=BC=4.
∵△APB为等腰直角三角形,
∴AP=BP,∠PAB=∠PBA=45°,
∴∠OAP=90°﹣∠PAB=45°,
∴△AOP为等腰直角三角形,
∴OA=OP=4.
t=4÷1=4(秒),
故t的值为4
(2)
解:∵△APB为等腰直角三角形,
∴∠APO+∠BPC=180°﹣90°=90°.
又∵∠PAO+∠APO=90°,
∴∠PAO=∠BPC.
在△PAO和△BPC中, 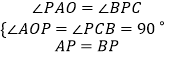 ,
,
∴△PAO≌△BPC,
∴AO=PC,BC=PO.
∵点A(0,4),点P(t,0),点B(x,y),
∴PC=AO=4,BC=PO=t=y,CO=PC+PO=4+y=x,
∴y=x﹣4
(3)
解:△APM为等腰三角形分三种情况:
①当AM=AP时,如图2所示.
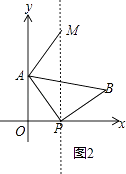
当t=3时,点P(3,0),
∵点M(3,a),点A(0,4),
∴由两点间的距离公式可知:
AM= ![]() ,AP=
,AP= ![]() =5,
=5,
∴ ![]() =5,解得:a=0(舍去),a=8.
=5,解得:a=0(舍去),a=8.
此时M点的坐标为(3,8);
②当MA=MP时,如图3所示.
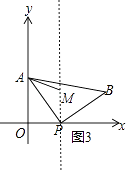
∵点P(3,0),点A(0,4),点M(3,a),
∴由两点间的距离公式可知:
MA= ![]() ,MP=a,
,MP=a,
∴ ![]() =a,解得:a=
=a,解得:a= ![]() .
.
此时M点的坐标为(3, ![]() );
);
③当PA=PM时,如图4所示.
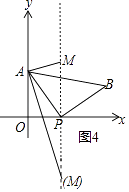
∵点P(3,0),点A(0,4),点M(3,a),
∴由两点间的距离公式可知:
PA= ![]() =5,PM=|a|,
=5,PM=|a|,
∴a=±5.
此时M点的坐标为(3,5)或(3,﹣5).
综上可知:当t=3时,平面直角坐标系内有一点M(3,a),使△APM为等腰三角形的点M的坐标为(3,8),(3, ![]() ),(3,5)和(3,﹣5)
),(3,5)和(3,﹣5)
【解析】(1)由AB∥x轴,可找出四边形ABCO为长方形,再根据△APB为等腰三角形可得知∠OAP=45°,从而得出△AOP为等腰直角三角形,由此得出结论;(2)先证出△PAO≌△BPC,即可得出各边的关系,利用坐标系中点的意义即可得出个线段的长度,由相等的量可得出结论;(3)由等腰三角形的性质可知,若△APM为等腰三角形只需找到一组临边相等即可,临边相等分三种情况,分类讨论结合两点间的距离公式即可得出结论.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】如图,点C是∠ABC一边上一点 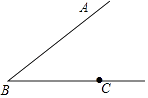
(1)按下列要求进行尺规作图: ①作线段BC的中垂线DE,E为垂足.
②作∠ABC的平分线BD.
③连结CD,并延长交BA于F.
(2)若∠ABC=62°,求∠BFC的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为开展好大课间活动,欲购买单价为20元的排球和单价为80元的篮球共100个.
(1)设购买排球数为x(个),购买两种球的总费用为y(元),请你写出y与x的函数关系式(不要求写出自变量的取值范围);
(2)如果购买两种球的总费用不超过6620元,并且篮球数不少于排球数的3倍,那么有哪几种购买方案?
(3)从节约开支的角度来看,你认为采用哪种方案更合算?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)化简后再求值: ![]() ,其中
,其中![]()
(2)若关于x、y的单项式cx2a+2y2与0.4xy3b+4的和为零,则![]() a2b-[
a2b-[![]() a2b-(3abc-a2c)-4a2c]-3abc的值又是多少?
a2b-(3abc-a2c)-4a2c]-3abc的值又是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某超市计划经销一些特产,经销前,围绕“A:王高虎头鸡,B:羊口咸蟹子,C:桂河芹菜,D:巨淀湖咸鸭蛋”四种特产,在全市范围内随机抽取了部分市民进行问卷调查:“我最喜欢的特产是什么?”(必选且只选一种).现将调查结果整理后,绘制成如图所示的不完整的扇形统计图和条形统计图.

(1)请补全扇形统计图和条形统计图;
(2)若全市有110万市民,估计全市最喜欢“羊口咸蟹子”的市民约有多少万人?
(3)在一个不透明的口袋中有四个分别写上四种特产标记A、B、C、D的小球(除标记外完全相同),随机摸出一个小球然后放回,混合摇匀后,再随机摸出一个小球,则两次都摸到A的概率是多少?写出分析计算过程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com