练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    15．下列运算正确的是（　　）
    A．（a3-a）÷a=a2B．（a3）2=a5C．a3+a2=a5D．a3÷a3=1

    分析 根据整式的除法、幂的乘方、同类项和同底数幂的除法计算判断即可．

    解答 解：A、（a3-a）÷a=a2-1，错误；
    B、（a3）2=a6，错误；
    C、a3与a2表示同类项，不能合并，错误；
    D、a3÷a3=1，正确；
    故选D．

    点评 此题考查整式的除法、幂的乘方、同类项和同底数幂的除法，关键是熟练掌握公式及法则进行计算．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：填空题

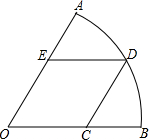    5．如图，扇形AOB的圆心角为60°，边长为$\sqrt{3}$的菱形OCDE的顶点C，E，D分别在OB，OA，弧AB上，则扇形AOB的面积为$\frac{3}{2}$π．（结果保留π）

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

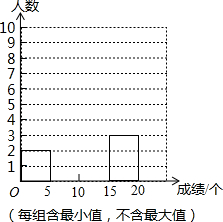    6．某校为了解九年级300名男生的体能情况，随机抽取了部分九年级男生进行“引体向上”测试，这些男生的测试成绩（单位：个）如下：
    9，12，3，13，18，8，8，4，10，12，13，■，9，8，12，13，18，13，12，10．
    其中有一数据被污损，统计员只记得这组数据的平均数是11．
    （1）求该组样本数据中被污损的数据和这组数据的众数；
    （2）请补充完整如图所示的频数分布直方图；
    （3）若规定完成10个以上（含10个）为体能达标，则估计该校九年级男生中有多少人体能达标？

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    3．如图，在平面直角坐标系xOy中，函数y=ax2+bx+1（a≠0）的图象与x的正半轴交于点A，与x的负半轴交于点B，与y轴交于点C．△PAC中，P（1，-1），∠P=90°，PA=PC．
    （1）求点A的坐标．
    （2）将△PAC沿AC翻折，若点P的对应点Q恰好落在函数y=ax2+bx+1（a≠0）的图象上，求a与b的值．
    （3）将△ACO绕点A逆时针旋转90°得到△ADE，在x轴上取一点M，将∠PMD沿PM翻折，若点D的对应点F恰好落在x轴上，求点M的坐标．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

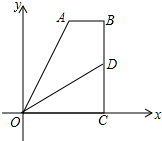    10．已知如图，在平面直角坐标系中，四边形ABCD的顶点A，B在第一象限，AB∥x轴，∠B=90°，AB+OC=OA，OD平分∠AOC交BC于点D．若四边形ABDO的面积为4，反比例函数y=$\frac{k}{x}$的图象经过点D，点A，则k的值是（　　）
    A．8B．6C．3D．4

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    20．函数y=$\sqrt{-3x+1}$中自变量x的取值范围是$x≤\frac{1}{3}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    7．如图1，在矩形ABCD中，AB=4cm，BC=8cm．E，F，G，H分别是AB，BC，CD，DA的中点，连结EF，FG，GH，HE．
    （1）求证：四边形EFGH是菱形；
    （2）如图2，若E1，E2分别从E出发以1cm/s的速度沿射线EA，EB方向运动，同时G1，G2从G出发以同样的速度分别沿射线GD，GC方向运动，E1F与E2H交于点M，G1F与G2H交于点N．设运动的时间为t（s），求四边形E1FG2H与四边形E2HG1F覆盖平面的总面积y与运动时间t之间的函数关系式；
    （3）当t为何值时，四边形HMFN为正方形．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    4．据2015年1月16日的渤海早报报道，2014年天津市公共交通客运量达1510000000人次，较2013年增长
    10.6%，将1510000000用科学记数法表示应为（　　）
    A．151×l07B．15.1×108C．15×l07D．1.51 xl09

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    5．一个圆锥的底面半径是5cm，其侧面展开图是圆心角是150°的扇形，则圆锥的母线长为（　　）
    A．9cmB．12cmC．15cmD．18cm

    查看答案和解析>>

    同步练习册答案