[题目]如图.在△ABC中.∠A=90°． (1)用直尺和圆规作出BC的垂直平分线(保留作图痕迹.不要求写作法),(2)BC的垂直平分线与AC相交于D.连结BD.若∠C=30°.则∠ABD= ．题目和参考答案——青夏教育精英家教网—

【题目】如图，在△ABC中，∠A=90°．
（1）用直尺和圆规作出BC的垂直平分线（保留作图痕迹，不要求写作法）；
（2）BC的垂直平分线与AC相交于D，连结BD，若∠C=30°，则∠ABD= ．

【答案】
（1）解：如图所示

（2）30°
【解析】解：（2）∵∠A=90°，∠C=30°， ∴∠ABC=60°，
∵DE是BC的垂直平分线，
∴BD=CD，
∴∠C=∠DBC=30°，
∴∠ABD=60°﹣30°=30°，
所以答案是：30°．
【考点精析】利用线段垂直平分线的性质对题目进行判断即可得到答案，需要熟知垂直于一条线段并且平分这条线段的直线是这条线段的垂直平分线；线段垂直平分线的性质定理：线段垂直平分线上的点和这条线段两个端点的距离相等．

练习册系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：初中数学 来源： 题型：

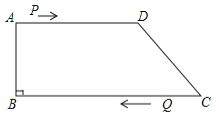
【题目】如图，在四边形ABCD中，AD∥BC，∠B=90°，AB=8cm，AD=12cm，BC=18cm，点P从点A出发以2cm/s的速度沿A→D→C运动，点P从点A出发的同时点Q从点C出发，以1cm/s的速度向点B运动，当点P到达点C时，点Q也停止运动．设点P，Q运动的时间为t秒．

（1）从运动开始，当t取何值时，PQ∥CD？

（2）从运动开始，当t取何值时，△PQC为直角三角形？

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】阅读：我们约定，在平面直角坐标系中，经过某点且平行于坐标轴或平行于两坐标轴夹角平分线的直线，叫该点的“特征线”．例如，点M（1，3）的特征线有：x=1，y=3，y=x+2，y=﹣x+4．

问题与探究：如图，在平面直角坐标系中有正方形OABC，点B在第一象限，A、C分别在x轴和y轴上，抛物线经过B、C两点，顶点D在正方形内部．

（1）直接写出点D（m，n）所有的特征线；

（2）若点D有一条特征线是y=x+1，求此抛物线的解析式；

（3）点P是AB边上除点A外的任意一点，连接OP，将△OAP沿着OP折叠，点A落在点A′的位置，当点A′在平行于坐标轴的D点的特征线上时，满足（2）中条件的抛物线向下平移多少距离，其顶点落在OP上？

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】某校进行书法比赛，有39名同学参加预赛，只能有19名同学参加决赛，他们预赛的成绩各不相同，其中一名同学想知道自己能否进入决赛，不仅要了解自己的预赛成绩，还要了解这39名同学预赛成绩的（　　）
A.平均数
B.中位数
C.方差
D.众数

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】我国南宋时期杰出的数学家杨辉是钱塘人，下面的图表是他在《详解九章算术》中记载的“杨辉三角”.此图揭示了（为非负整数）的展开式的项数及各项系数的有关规律.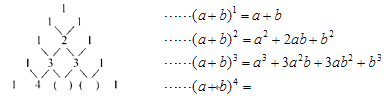

（1）请仔细观察，填出(a＋b)4的展开式中所缺的系数．(a＋b)4＝a4＋4a3b＋a2b2＋4ab2＋b4
（2）此规律还可以解决实际问题：假如今天是星期三，再过7天还是星期三，那么再过天是星期．