
 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案科目:初中数学 来源: 题型:
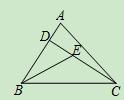
如图,已知在△ABC中,CD是AB边上的高线,BE平分∠ABC,交CD于点E,BC=5,DE=2,则△BCE的面积等于( )
A. 10 B. 7 C. 5 D. 4
B. 7 C. 5 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
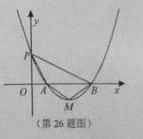
若关于x的二次函数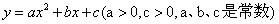 与x轴交于两个不同的点
与x轴交于两个不同的点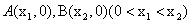 ,与y轴交于点P,其图像顶点为点M,点O为坐标原点。
,与y轴交于点P,其图像顶点为点M,点O为坐标原点。
(1)当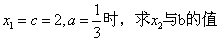 ;
;
(2)当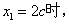 试问△ABM能否为等边三角形?判断并证明你的结论;
试问△ABM能否为等边三角形?判断并证明你的结论;
(3)当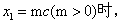 记△MAB,△PAB的面积分别为S1,S2,若△BPO∽△PAO,且S1=S2,求m的值。
记△MAB,△PAB的面积分别为S1,S2,若△BPO∽△PAO,且S1=S2,求m的值。
查看答案和解析>>
科目:初中数学 来源: 题型:
设二次函数y1=a(x−x1)(x−x2)(a≠0,x1≠x2)的图象与一次函数y2=dx+e(d≠0)的图象交于点(x1,0),若函数y=y2+y1的图象与x轴仅有一个交点,则( )
)
A. a(x1−x2)=d B. a(x2−x1)=d C. a(x 1−x2)2=d D. a(x1+x2)2=d
1−x2)2=d D. a(x1+x2)2=d
查看答案和解析>>
科目:初中数学 来源: 题型:
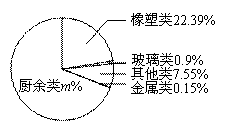
杭州市推行垃圾分类已经多年,但在厨余垃圾中除了厨余类垃圾还混杂着非厨余类垃 圾,如图是杭州市某一天收到的厨余垃圾的统计图
圾,如图是杭州市某一天收到的厨余垃圾的统计图
1) 试求出m的值
2) 杭州市那天共收到厨余垃圾约200吨,请计算其中混杂着的玻璃类垃圾的吨数
查看答案和解析>>
科目:初中数学 来源: 题型:
定义:长宽比为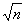 :1(n为正基数)的矩形称为株为
:1(n为正基数)的矩形称为株为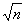 矩形. 下面,我们通过折叠的方式折出一个
矩形. 下面,我们通过折叠的方式折出一个 矩形.
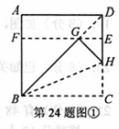
矩形. 如图①所示.
如图①所示.
操作1:将正方形ABCD沿过点B的直线折叠,使折叠后的点C落在对角线BD上的点G处,折痕为BH
操作2:将AD沿过点G的直线折叠,使点A,点D分别落在边AB,CD上,折痕为EF
则四 边形BCEF为
边形BCEF为 矩形
矩形
证明:设正方形ABCD的边长为1,则BD=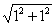 =
= .
.
由折叠性质可知BG=BC=1,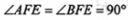 ,则四边形BCEF为矩形
,则四边形BCEF为矩形

阅读以上内容,回答下列问题:
(1) 在图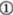 中,所有与CH相等的线段是 ,tan
中,所有与CH相等的线段是 ,tan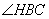 的值是
的值是
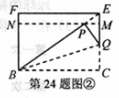
(2) 已知四边形BCEF为 矩形,模仿上述操作,得到四边形BCMN,如图
矩形,模仿上述操作,得到四边形BCMN,如图 。
。
求证:四边形BCMN是 矩形
矩形
将图 中的
中的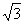 矩形BCM
矩形BCM N沿用(2)中的操作3次后,得到一个“
N沿用(2)中的操作3次后,得到一个“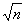 矩形”,则n的值是
矩形”,则n的值是
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com