
【题目】如图,平行于x轴的直线AC分别交抛物线y1=x2(x≥0)与y2= ![]() (x≥0)于B、C两点,过点C作y轴的平行线交y1于点D,直线DE∥AC,交y2于点E,则
(x≥0)于B、C两点,过点C作y轴的平行线交y1于点D,直线DE∥AC,交y2于点E,则 ![]() = .
= . 
【答案】![]()
【解析】解:设A点坐标为(0,a),(a>0),
则x2=a,解得x= ![]() ,
,
∴点B( ![]() ,a),
,a), ![]() =a,
=a,
则x= ![]() a,
a,
∴点C( ![]() a,a),
a,a),
∴BC= ![]() a﹣
a﹣ ![]() .
.
∵CD∥y轴,
∴点D的横坐标与点C的横坐标相同,为 ![]() a,
a,
∴y1=( ![]() a)2=3a,
a)2=3a,
∴点D的坐标为( ![]() a,3a).
a,3a).
∵DE∥AC,
∴点E的纵坐标为3a,
∴ ![]() =3a,
=3a,
∴x=3 ![]() ,
,
∴点E的坐标为(3 ![]() ,3a),
,3a),
∴DE=3 ![]() ﹣
﹣ ![]() a,
a,
∴ ![]() =
= ![]() =
= ![]() .
.
故答案是: ![]() .
.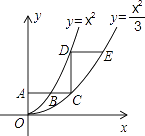
【考点精析】关于本题考查的二次函数的图象和二次函数的性质,需要了解二次函数图像关键点:1、开口方向2、对称轴 3、顶点 4、与x轴交点 5、与y轴交点;增减性:当a>0时,对称轴左边,y随x增大而减小;对称轴右边,y随x增大而增大;当a<0时,对称轴左边,y随x增大而增大;对称轴右边,y随x增大而减小才能得出正确答案.


科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,⊙M与x轴相切于点A(8,0),与y轴分别交于点B(0,4)和点C(0,16),则圆心M到坐标原点O的距离是( ) 
A.10
B.8 ![]()
C.4 ![]()
D.2 ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】请阅读下列材料,并完成相应的任务。
阿基米德(Archimedes,公元前287~公元前212年,古希腊)是有史以来最伟大的数学家之一.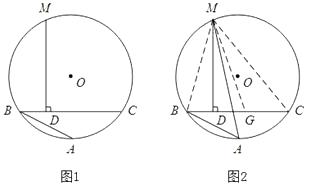
阿基米德折弦定理:如图1,AB和BC是圆O的两条弦(即折线ABC是圆的一条折弦), BC>AB,M是 ![]() 的中点,即CD=AB+BD。下面是运用“截长法”证明CD=AB+BD的部分过程。
的中点,即CD=AB+BD。下面是运用“截长法”证明CD=AB+BD的部分过程。
证明:如图2,在CB上截取CG=AB,连接MA、MB、MC、MG。因为M是弧ABC的中点,所以MA=MC.
任务:
(1)请按照上面的证明思路,完整证明阿基米德折弦定理,即CD=AB+BD。
(2)如图3,已知等边△ABC内接于圆O,AB=1,D为 ![]() 上一点,∠ABD=45°,AE⊥BD于点E,则△BDC的周长是.
上一点,∠ABD=45°,AE⊥BD于点E,则△BDC的周长是.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一慢车和一快车沿相同路线从A地到B地,所行驶的路程与时间的函数图象如图所示,试根据图象回答下列问题:

(1)由图象你可以得到哪些信息?
(2)求慢车、快车的速度.
(3)求A,B两地之间的距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△BAD是由△BEC在平面内绕点B旋转60°而得,且AB⊥BC,BE=CE,连接DE. 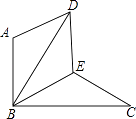
(1)求证:△BDE≌△BCE;
(2)试判断四边形ABED的形状,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,将四边形ABCD称为“基本图形”,且各点的坐标分别为A(4,4),B(1,3),C(3,3),D(3,1).
①画出“基本图形”关于原点O对称的四边形A1B1C1D1 , 并填出A1 , B1 , C1 , D1的坐标;
②画出“基本图形”绕B点顺时针旋转90°所成的四边形A2B2C2D2
A1( , )B1( , )
C1( , )D1( , )
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】仔细阅读下面的例题:
例题:已知二次三项式x2-4x+m有一个因式是x+3,求另一个因式以及m的值.
解:设另一个因式为x+n,则
x2-4x+m=(x+3)(x+n),
∴x2-4x+m=x2+(n+3)x+3n,
∴![]() ,解得
,解得![]() ,
,
∴另一个因式为x-7,m的值为-21.
问题:仿照以上方法解答下面的问题:
已知二次三项式2x2+3x-k有一个因式是2x-5,求另一个因式以及k的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线y=﹣ ![]() x2﹣
x2﹣ ![]() x+2与x轴交于A、B两点,与y轴交于点C
x+2与x轴交于A、B两点,与y轴交于点C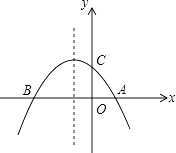
(1)求点A,B,C的坐标;
(2)点E是此抛物线上的点,点F是其对称轴上的点,求以A,B,E,F为顶点的平行四边形的面积;
(3)此抛物线的对称轴上是否存在点M,使得△ACM是等腰三角形?若存在,请求出点M的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD与正方形AEFG起始时互相重合,现将正方形AEFG绕点A逆时针旋转,设旋转角∠BAE=α(0°<α<360°),则当正方形的顶点F落在正方形的对角线AC或BD所在直线上时,α= . 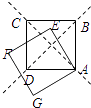
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com