
【题目】如图,正方形ABCD与正方形AEFG起始时互相重合,现将正方形AEFG绕点A逆时针旋转,设旋转角∠BAE=α(0°<α<360°),则当正方形的顶点F落在正方形的对角线AC或BD所在直线上时,α= . 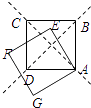
【答案】60°或180°
【解析】解:依照题意画出图形,如图所示. 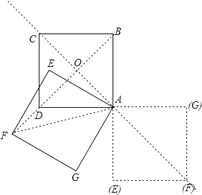
①当点F在BD上时:令AC、BD的交点为O,设正方形ABCD的边长为2a,
则AC=AF=2 ![]() a,AO=
a,AO= ![]() AC=
AC= ![]() a.
a.
∵四边形ABCD为正方形,
∴AC⊥BD,∠BAC=∠DAC=∠EAF=45°,
∴∠AOF=90°.
在Rt△AOF中,AO= ![]() a,AF=2
a,AF=2 ![]() a,
a,
∴cos∠OAF= ![]() =
= ![]() ,
,
∴∠OAF=60°,∠OAE=∠OAF﹣∠EAF=15°,
∴α=∠BAE=∠BAC+∠OAE=60°;
②当点F在AC上时,
∵C、A、F三点共线,∠EAF=∠BAC=45°,
∴B、A、E三点共线,
∴α=∠BAE=180°.
综上可知:当正方形的顶点F落在正方形的对角线AC或BD所在直线上时,α=60°或180°.
所以答案是:60°或180°.
【考点精析】本题主要考查了正方形的性质和旋转的性质的相关知识点,需要掌握正方形四个角都是直角,四条边都相等;正方形的两条对角线相等,并且互相垂直平分,每条对角线平分一组对角;正方形的一条对角线把正方形分成两个全等的等腰直角三角形;正方形的对角线与边的夹角是45o;正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形;①旋转后对应的线段长短不变,旋转角度大小不变;②旋转后对应的点到旋转到旋转中心的距离不变;③旋转后物体或图形不变,只是位置变了才能正确解答此题.


科目:初中数学 来源: 题型:
【题目】如图,平行于x轴的直线AC分别交抛物线y1=x2(x≥0)与y2= ![]() (x≥0)于B、C两点,过点C作y轴的平行线交y1于点D,直线DE∥AC,交y2于点E,则
(x≥0)于B、C两点,过点C作y轴的平行线交y1于点D,直线DE∥AC,交y2于点E,则 ![]() = .
= . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了庆祝即将到来的2018年国庆节,某校举行了书法比赛,赛后整理了参赛同学的成绩,并制作了如下两幅不完整的统计图表
分数段 | 频数 | 频率 |
60≤x<70 | 30 | 0.15 |
70≤x<80 | m | 0.45 |
80≤x<90 | 60 | n |
90≤x<100 | 20 | 0.1 |
请根据以上图表提供的信息,解答下列问题:
(1)这次共调查了 名学生;表中的数m= ,n= .
(2)请补全频数直方图;
(3)若绘制扇形统计图,则分数段60≤x<70所对应的扇形的圆心角的度数是 .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某产品每件的成本为10元,在试销阶段每件产品的日销售价x(元)与产品的日销售量y(件)之间的关系如下表:
X(元) | 15 | 20 | 25 | … |
Y(件) | 25 | 20 | 15 | … |
(1)观察与猜想y与x的函数关系,并说明理由.
(2)求日销售价定为30元时每日的销售利润.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】直角坐标系中,已知点P(﹣2,﹣1),点T(t,0)是x轴上的一个动点. 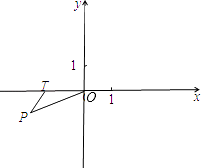
(1)求点P关于原点的对称点P′的坐标;
(2)当t取何值时,△P′TO是等腰三角形?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知2辆A型车和1辆B型车载满货物一次可运货10吨.用1辆A型车和2辆B型车载满货物一次可运货11吨.某物流公司现有31吨货物,计划同时租用A型车a辆和B型车b辆,一次运完,且每辆车都满载货物.根据以上信息解答下列问题:
(1)1辆A型车和1辆B型车载满货物一次分别可运货物多少吨?
(2)请帮助物流公司设计租车方案
(3)若A型车每辆车租金每次100元,B型车每辆车租金每次120元.请选出最省钱的租车方案,并求出最少的租车费.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某日,正在我国南海海域作业的一艘大型渔船突然发生险情,相关部门接到求救信号后,立即调遣一架直升飞机和一艘刚在南海巡航的渔政船前往救援.当飞机到达距离海面3000米的高空C处,测得A处渔政船的俯角为60°,测得B处发生险情渔船的俯角为30°,请问:此时渔政船和渔船相距多远?(结果保留根号) 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】班主任要从甲、乙两名跳远运动员中挑选一人参加校运动会比赛.在最近的10次选拔赛中,他们的成绩如下(单位:cm):
甲 | 585 | 596 | 610 | 598 | 612 | 597 | 604 | 600 | 613 | 601 |
乙 | 613 | 618 | 580 | 574 | 618 | 593 | 585 | 590 | 598 | 624 |
(1)他们的平均成绩分别是多少?
(2)甲、乙两名运动员这10次比赛成绩的极差、方差分别是多少?
(3)怎样评价这两名运动员的运动成绩?
(4)历届比赛表明,成绩达到5.96m就有可能夺冠,你认为为了夺冠应选择谁参加这项比赛?如果历届比赛成绩表明,成绩达到6.10m就能打破记录,那么你认为为了打破记录应选择谁参加这项比赛?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com