【题目】如图
和
的平分线交于点
的延长线交
于点
.
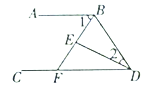
（1）求证：
；
（2）如果
，那么
等于多少度？
【答案】(1)见解析;(2)120°.
【解析】
（1）依据平行线的性质，以及角平分线的定义，即可得到∠1+∠2=
（∠ABD+∠BDC），进而得出结论；
（2）依据角平分线定义以及（1）中的结论，即可得出∠1=60°，再根据平行线的性质，即可得到∠BFC的度数．
（1）证明：∵AB∥CD，
∴∠ABD+∠BDC=180°，
∵BE、DE分别平分∠ABD、∠BDC，
∴∠1=∠ABD，∠2=∠BDC，
∴∠1+∠2=（∠ABD+∠BDC）=90°，
（2）解：∵DE平分∠BDC，BF平分∠ABD,
∴∠2=∠EDF=30°，∠1=∠FBD,
又∵∠1+∠2=90°，
∴∠1=60°，
∵AB∥CD，
∴∠BFC=180°-∠1=180°-60°=120°．
科目：初中数学 来源： 题型：
【题目】对于平面直角坐标系
中的图形M和点P（点P在M内部或M上），给出如下定义：
如果图形M上存在点Q，使得
，那么称点P为图形M的和谐点．
已知点
，
，
，
．
（1）在点
，
，
中，矩形
的和谐点是_________________；
（2）如果直线
上存在矩形的和谐点P，求出点P的横坐标t的取值范围；
（3）如果直线
上存在矩形的和谐点E，F，使得线段
上的所有点（含端点）都是矩形的和谐点，且
，求出b的取值范围．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】某企业前年按可回收垃圾处理费15元/吨、不可回收垃圾处理费25元/吨的收费标准，共支付两种垃圾处理费5000元，从去年元月起，收费标准上调为：可回收垃圾处理费30元/吨，不可回收垃圾处理费100元/吨．若该企业去年处理的这两种垃圾数量与前年相比没有变化，但调价后就要多支付处理费9000元．
（1）该企业前年处理的可回收垃圾和不可回收垃圾各多少吨？
（2）该企业计划今年将上述两种垃圾处理总量减少到200吨，且可回收垃圾不少于不可回收垃圾处理量的3倍，则今年该企业至少有多少吨可回收垃圾？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】某地震救援队探测出某建筑物废墟下方点C处有生命迹象，已知废墟一侧地面上两探测点A，B相距3米，探测线与地面的夹角分别是30°和60°（如图），试确定生命所在点C的深度．（结果保留根号）
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】有若干个仅颜色不同的红球和黑球，现往一个不透明的袋子里装进4个红球和6个黑球.
（1）若先从袋子里取出m个红球（不放回），再从袋子里随机摸出一个球，将“摸到黑球”记为事件A. 若事件A为必然事件，则m= .
（2）若先从袋子里取出n个黑球，再放入2n个红球，若随机摸出一个球是红球的概率等于2/3，通过计算求n的值.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】为开展全科大阅读活动，学校花费了3400元在书店购买了40套古典文学书籍和20套现代文学书籍，每套现代文学书籍比每套古典文学书籍多花20元.
（1）求每套古典文学习书籍和现代文学书籍分别是多少元？
（2）为满足学生的阅读需求，学校计划用不超过2500元再次购买古典文学和现代文学书籍共40套，经市场调查得知，每套古典文学书籍价格上浮了20%，每套现代文学书籍价格下调了10%，学校最多能购买多少套现代文学书籍？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】周末，小梅骑自行车去外婆家，从家出发
小时后到达甲地，在甲地游玩一段时间后，按原速继续前进，小梅出发
小时后，爸爸骑摩托车沿小梅骑自行车的路线追赶小梅，如图是他们离家的路程
（千米）与小梅离家时间
（小时）的关系图，已知爸爸骑摩托车的速度是小梅骑自行车速度的
倍。
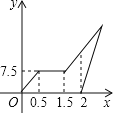
（1）小梅在甲地游玩时间是_________小时，小梅骑车的速度是_________千米/小时.
（2）若爸爸与小梅同时到达外婆家，求小梅家到外婆家的路程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
