
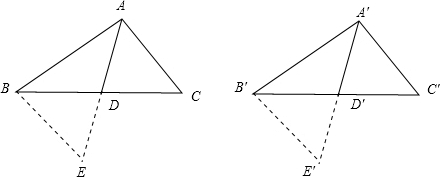
 证明:如图,延长AD到点E使AD=DE,连接BE,延长A′D′到点E′使A′D′=D′E′,
证明:如图,延长AD到点E使AD=DE,连接BE,延长A′D′到点E′使A′D′=D′E′,
|
|
|


 新思维假期作业寒假吉林大学出版社系列答案
新思维假期作业寒假吉林大学出版社系列答案科目:初中数学 来源: 题型:
 如图所示,在O点的观测站测得渔船A、B的方向分别为北偏东45°,南偏西30°,为了减少相互干扰并取得较好的捕鱼效益,渔船C恰好位于∠AOB的平分线上,求渔船C相对观测站的方向.
如图所示,在O点的观测站测得渔船A、B的方向分别为北偏东45°,南偏西30°,为了减少相互干扰并取得较好的捕鱼效益,渔船C恰好位于∠AOB的平分线上,求渔船C相对观测站的方向.查看答案和解析>>
科目:初中数学 来源: 题型:
| A、和为180°的两个角互为邻补角 |
| B、有公共顶点且互补的两个角互为邻补角 |
| C、有一条公共边且有一条公共边,另一边互为反向延长线的两个角互为邻补角 |
| D、有公共顶点且有一条公共边,另一边互为反向延长线的两个角互为邻补角 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com