
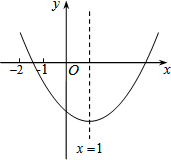 已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,有下列结论:
已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,有下列结论:| A. | 5 | B. | 4 | C. | 3 | D. | 2 |
分析 由抛物线的开口方向判断a与0的关系,由抛物线与y轴的交点判断c与0的关系,然后根据对称轴及抛物线与x轴交点情况进行推理,进而对所得结论进行判断.
解答 解:①由图知:抛物线与x轴有两个不同的交点,则△=b2-4ac>0,故①正确;
②抛物线开口向上,得:a>0;
抛物线的对称轴为x=-$\frac{b}{2a}$=1,b=-2a,故b<0;
抛物线交y轴于负半轴,得:c<0;
所以abc>0;
故②正确;
③∵x=-$\frac{b}{2a}$=1,
∴2a+b=0,故③错误;
④观察图象得当x=3时,y>0,
即9a+3b+c>0,故④错误;
⑤∵b=-2a,
∴9a+3b+c=9a-6a+c=3a+c>0
∵a>0
∴8a+c>0,故⑤正确,
所以①②⑤这四个结论都正确.
故选C.
点评 本题主要考查图象与二次函数系数之间的关系,关键是根据对称轴求2a与b的关系,以及二次函数与方程之间的转换,根的判别式等.


科目:初中数学 来源: 题型:解答题
 在?ABCD中,E为BC的中点,过点E作EF⊥AB于点F,延长DC,交FE的延长线于点G,连结DF,已知∠FDG=45°
在?ABCD中,E为BC的中点,过点E作EF⊥AB于点F,延长DC,交FE的延长线于点G,连结DF,已知∠FDG=45°查看答案和解析>>
科目:初中数学 来源: 题型:填空题
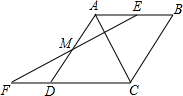 如图,点E在菱形ABCD边上,AE=1,过E作AC的垂线EF,交AD于点M,交CD的延长线于点F,DF=2,∠B=60°,点P是AC上的动点,则PM+PF的最小值3$\sqrt{3}$.
如图,点E在菱形ABCD边上,AE=1,过E作AC的垂线EF,交AD于点M,交CD的延长线于点F,DF=2,∠B=60°,点P是AC上的动点,则PM+PF的最小值3$\sqrt{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
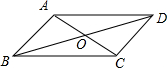 如图,平行四边形ABCD的对角线AC,BD交于点O,AC⊥AB,AB=2,且AC:BD=1:2,
如图,平行四边形ABCD的对角线AC,BD交于点O,AC⊥AB,AB=2,且AC:BD=1:2,查看答案和解析>>
科目:初中数学 来源: 题型:填空题
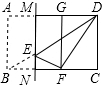 如图,在矩形ABCD中,AB=6,BC=8,点E是对角线BD上一动点(不与点B、D重合),将矩形沿过点E的直线MN折叠,使得点A、B的对应点G、F分别在直线AD与BC上,当△DEF为直角三角形时,CN的长为$\frac{25}{4}$或$\frac{7}{4}$.
如图,在矩形ABCD中,AB=6,BC=8,点E是对角线BD上一动点(不与点B、D重合),将矩形沿过点E的直线MN折叠,使得点A、B的对应点G、F分别在直线AD与BC上,当△DEF为直角三角形时,CN的长为$\frac{25}{4}$或$\frac{7}{4}$.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
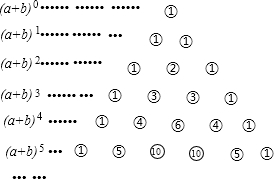
| A. | 2017 | B. | 2016 | C. | 191 | D. | 190 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
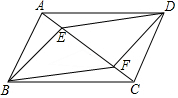 如图,在四边形ABCD中,AB∥CD,点E、F是对角线AC上两点,且∠ABF=∠CDE,AE=CF
如图,在四边形ABCD中,AB∥CD,点E、F是对角线AC上两点,且∠ABF=∠CDE,AE=CF查看答案和解析>>
科目:初中数学 来源: 题型:选择题
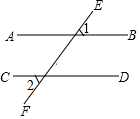 如图,直线AB,CD被直线EF所截,∠1=55°,下列条件中能判定AB∥CD的是( )
如图,直线AB,CD被直线EF所截,∠1=55°,下列条件中能判定AB∥CD的是( )| A. | ∠2=35° | B. | ∠2=45° | C. | ∠2=55° | D. | ∠2=125° |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
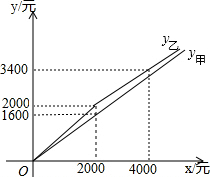 江汉平原享有“中国小龙虾之乡”的美称,甲、乙两家农贸商店,平时以同样的价格出售品质相同的小龙虾.“龙虾节”期间,甲、乙两家商店都让利酬宾,付款金额y甲、y乙(单位:元)与原价x(单位:元)之间的函数关系如图所示.
江汉平原享有“中国小龙虾之乡”的美称,甲、乙两家农贸商店,平时以同样的价格出售品质相同的小龙虾.“龙虾节”期间,甲、乙两家商店都让利酬宾,付款金额y甲、y乙(单位:元)与原价x(单位:元)之间的函数关系如图所示.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com