
【题目】如图,在△ABC中,∠BAC=120°,AB=AC=4,AD⊥BC,BD=2![]() ,延长AD到E,使AE=2AD,连接BE.
,延长AD到E,使AE=2AD,连接BE.
(1)求证:△ABE为等边三角形;
(2)将一块含60°角的直角三角板PMN如图放置,其中点P与点E重合,且∠NEM=60°,边NE与AB交于点G,边ME与AC交于点F.求证:BG=AF;
(3)在(2)的条件下,求四边形AGEF的面积.

【答案】(1)见解析;(2)见解析;(3)4![]()
【解析】试题分析:(1)先证明![]() ,可知AB=2AD,因为AE=2AD,所以AB=AE,从而可知△ABE是等边三角形.
,可知AB=2AD,因为AE=2AD,所以AB=AE,从而可知△ABE是等边三角形.
(2)由(1)可知: ![]() AE=BE,然后求证
AE=BE,然后求证![]() 即可得出BG=AF;
即可得出BG=AF;
(3)由于∴S四边形![]() 故只需求出△ABE的面积即可.
故只需求出△ABE的面积即可.
试题解析:
(1)AB=AC,AD⊥BC,
![]()
![]()
∴AB=2AD,
∵AE=2AD,
∴AB=AE,
![]()
∴△ABE是等边三角形.
(2)∵△ABE是等边三角形,
![]()
AE=BE,
由(1) ![]()
∴∠ABE=∠CAE,
![]()
∴∠NEM∠AEN=∠BEA∠AEN,
∴∠AEF=∠BEG,
在△BEG与△AEF中,

![]()
∴BG=AF;
(3)由(2)可知: ![]()
![]()
∴S四边形![]()
∵△ABE是等边三角形,
∴AE=AB=4,
![]()
∴S四边形![]()


 计算高手系列答案
计算高手系列答案科目:初中数学 来源: 题型:
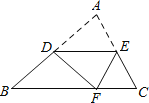
【题目】如图,在△ABC中,∠A=70°∠B=50°,点D,E分别为AB,AC上的点,沿DE折叠,使点A落在BC边上点F处,若△EFC为直角三角形,则∠BDF的度数为______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,![]() 城市在
城市在![]() 城市正东方向,现计划在
城市正东方向,现计划在![]() 两城市间修建一条高速铁路(即线段
两城市间修建一条高速铁路(即线段![]() ),经测量,森林保护区的中心
),经测量,森林保护区的中心![]() 在城市
在城市![]() 的北偏东
的北偏东![]() 方向上,在线段
方向上,在线段![]() 上距
上距![]() 城市
城市![]() 的
的![]() 处测得
处测得![]() 在北偏东
在北偏东![]() 方向上,已知森林保护区是以点
方向上,已知森林保护区是以点![]() 为圆心,
为圆心,![]() 为半径的圆形区域,请问计划修建的这条高速铁路是否穿越保护区,为什么?
为半径的圆形区域,请问计划修建的这条高速铁路是否穿越保护区,为什么?
(参考数据:![]() )
)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法中,错误的是( )
A. 二次函数![]() 的图象是开口向上的抛物线
的图象是开口向上的抛物线
B. 二次函数![]() 的图象必在
的图象必在![]() 轴上方
轴上方
C. 二次函数图象的对称轴是![]() 轴或与
轴或与![]() 轴平行的直线
轴平行的直线
D. 二次函数图象的顶点必在图象的对称轴上
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】人民商场销售某种商品,统计发现:每件盈利![]() 元时,平均每天可销售
元时,平均每天可销售![]() 件.经调查发现,该商品每降价
件.经调查发现,该商品每降价![]() 元,商场平均每天可多售出
元,商场平均每天可多售出![]() 件.
件.
![]() 假如现在库存量太大,部门经理想尽快减少库存,又想销售该商品日盈利达到
假如现在库存量太大,部门经理想尽快减少库存,又想销售该商品日盈利达到![]() 元,请你帮忙思考,该降价多少?
元,请你帮忙思考,该降价多少?
![]() 假如部门经理想销售该商品的日盈利达到最大,请你帮忙思考,又该如何降价?
假如部门经理想销售该商品的日盈利达到最大,请你帮忙思考,又该如何降价?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图,边长为a、b的矩形,它的周长为14,面积为10,求a2b+3a3b3+ab2的值;

(2)已知a+b=8,ab=16+c2,求(a﹣b+c)2018的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
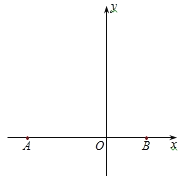
【题目】如图所示,已知等边△ABC的两个顶点的坐标为A(-4,0),B(2,0).
(1)用尺规作图作出点C,并求出点C的坐标;
(2)求△ABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=ax2+bx+c过点A(0,2),且抛物线上任意不同两点M(x1,y1),N(x2,y2)都满足:当x1<x2<0时,(x1﹣x2)(y1﹣y2)>0;当0<x1<x2时,(x1﹣x2)(y1﹣y2)<0.以原点O为圆心,OA为半径的圆与抛物线的另两个交点为B,C,且B在C的左侧,△ABC有一个内角为60°.
(1)求抛物线的解析式;
(2)若MN与直线y=﹣2![]() x平行,且M,N位于直线BC的两侧,y1>y2,解决以下问题:
x平行,且M,N位于直线BC的两侧,y1>y2,解决以下问题:
①求证:BC平分∠MBN;
②求△MBC外心的纵坐标的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com