
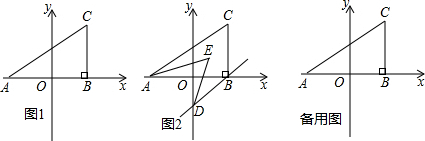
分析 (1)根据非负数的性质易得a=-4,b=4,然后根据三角形面积公式计算;
(2)分类讨论:设P(0,t),当P在y轴正半轴上时,过P作MN∥x轴,AN∥y轴,BM∥y轴,利用S△APC=S梯形MNAC-S△ANP-S△CMP=8可得到关于t的方程,再解方程求出t;
(3)过E作EF∥AC,根据平行线性质得BD∥AC∥EF,且∠3=$\frac{1}{2}$∠CAB=∠1,∠4=$\frac{1}{2}$∠ODB=∠2,所以∠AED=∠1+∠2=$\frac{1}{2}$(∠CAB+∠ODB);然后把∠CAB+∠ODB=∠5+∠6=90° 代入计算即可.
解答 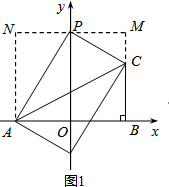 解:(1)∵(a+4)2+$\sqrt{b-4}$=0,
解:(1)∵(a+4)2+$\sqrt{b-4}$=0,
∴a+4=0,b-4=0,
∴a=-4,b=4,
∵CB⊥AB
∴A(-4,0),B(4,0),C(4,2),
∴△ABC的面积=$\frac{1}{2}$×2×8=8;
(2)①当P在y轴正半轴上时,如图1,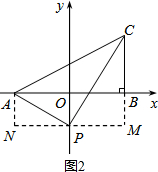
设P(0,t),
过P作MN∥x轴,AN∥y轴,BM∥y轴,
∵S△APC=S梯形MNAC-S△ANP-S△CMP=8,
∴$\frac{1}{2}$×8×(t+t-2)-$\frac{1}{2}$×4t-$\frac{1}{2}$×4×(t-2)=8,
解得:t=3,
②当P在y轴负半轴上时,如图2,
∵S△APC=S梯形MNAC-S△ANP-S△CMP=8
∴$\frac{1}{2}$×8(-t+2-t)+$\frac{1}{2}$×4t-$\frac{1}{2}$×4(2-t)=8,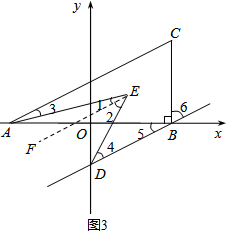
解得:t=-1,
∴P(0,-1)或(0,3).
(3)∵CB∥y轴,BD∥AC,
∴∠CAB=∠5,∠ODB=∠6,∠CAB+∠ODB=∠5+∠6=90°,
过E作EF∥AC,如图3,
∵BD∥AC,
∴BD∥AC∥EF,
∵AE,DE分别平分∠CAB,∠ODB,
∴∠3=$\frac{1}{2}$∠CAB=∠1,∠4=$\frac{1}{2}$∠ODB=∠2,
∴∠AED=∠1+∠2=$\frac{1}{2}$(∠CAB+∠ODB)=45°.
点评 本题考查了平行线的判定与性质:两直线平行,内错角相等.也考查了非负数的性质、坐标与图形性质以及三角形面积公式.


 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案科目:初中数学 来源: 题型:解答题
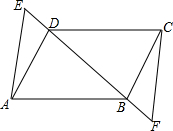 如图,在四边形ABCD中,点E、F在直线BD上,AE=CF,AD=CB,BE=DF.
如图,在四边形ABCD中,点E、F在直线BD上,AE=CF,AD=CB,BE=DF.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
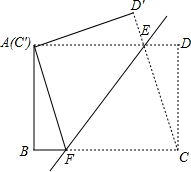 如图,将矩形ABCD沿直线EF折叠,使点C与点A重合,折痕交AD于点E、交BC于点F,连接AF、CE.①AF=CD′;②△CEF是等腰三角形;③四边形AFCE为菱形;④设AE=a,ED=b,DC=c,则a、b、c三者之间的数量关系为a2=b2+c2,其中正确的结论是②③④(将所有正确结论的序号都填在横线上)
如图,将矩形ABCD沿直线EF折叠,使点C与点A重合,折痕交AD于点E、交BC于点F,连接AF、CE.①AF=CD′;②△CEF是等腰三角形;③四边形AFCE为菱形;④设AE=a,ED=b,DC=c,则a、b、c三者之间的数量关系为a2=b2+c2,其中正确的结论是②③④(将所有正确结论的序号都填在横线上)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
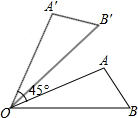 如图,可以看到点A旋转到点A′,OA旋转到OA′,∠AOB旋转到∠A′OB′,这些都是互相对应的点、线段与角.那么,线段AB的对应线段是线段A′B′;线段OB的对应线段是线段OB′;∠A的对应角是∠A′.
如图,可以看到点A旋转到点A′,OA旋转到OA′,∠AOB旋转到∠A′OB′,这些都是互相对应的点、线段与角.那么,线段AB的对应线段是线段A′B′;线段OB的对应线段是线段OB′;∠A的对应角是∠A′.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com