
【题目】如图1,直线![]() 与
与![]() 轴交于点
轴交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,直线
,直线![]() 交
交![]() 轴于点
轴于点![]() ,将
,将![]() 沿直线
沿直线![]() 折叠,点
折叠,点![]() 恰好落在直线
恰好落在直线![]() 上的点
上的点![]() 处.
处.
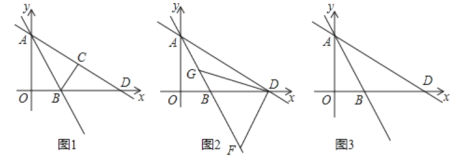
(1)求![]() 的长;
的长;
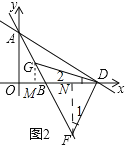
(2)如图2,![]() ,
,![]() 是直线
是直线![]() 上的两点,若
上的两点,若![]() 是以
是以![]() 为斜边的等腰直角三角形,求点
为斜边的等腰直角三角形,求点![]() 的坐标;
的坐标;
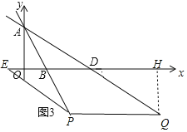
(3)如图3,点![]() 是直线
是直线![]() 上一点,点
上一点,点![]() 是直线
是直线![]() 上一点,且
上一点,且![]() ,
,![]() 均在第四象限,点
均在第四象限,点![]() 是
是![]() 轴上一点,若四边形
轴上一点,若四边形![]() 为菱形,求点
为菱形,求点![]() 的坐标.
的坐标.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]()
【解析】
(1)设BC=OB=x,则BD=8x,在Rt△BCD中,根据BC2+CD2=BD2,构建方程即可解决问题;
(2)作GM⊥x轴于M,FN⊥x轴于N,由△DMG≌△FND(AAS),推出GM=DN,DM=FN,设GM=DM=m,DM=FN=n,根据G、F在直线AB上,构建方程组即可解决问题;
(3)如图,设Q(a,![]() a+6),因为PQ∥x轴,且点P在直线y=2x+6上,推出P(
a+6),因为PQ∥x轴,且点P在直线y=2x+6上,推出P(![]() a,
a,![]() a+6),PQ=
a+6),PQ=![]() a,作QH⊥x轴于H.由勾股定理可知:QH:DH:DQ=3:4:5,想办法构建方程即可解决问题.
a,作QH⊥x轴于H.由勾股定理可知:QH:DH:DQ=3:4:5,想办法构建方程即可解决问题.
(1)对于直线![]() ,令
,令![]() ,得到
,得到![]() ,可得
,可得![]() ,
,
令![]() ,得到
,得到![]() ,可得
,可得![]() ,
,
∴![]() ,
,![]() ,
,![]() ,
,
∴![]() ,设
,设![]() ,则
,则![]() ,
,
在![]() 中,∵
中,∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() .
.
(2)设直线![]() 的解析式为
的解析式为![]() ,
,
∵![]() ,即
,即![]() ,
,
∴把![]() 代入
代入![]() 得,
得,
∴![]() ,
,
∴![]() ,
,
∴直线![]() 的解析式为
的解析式为![]() ,
,
作![]() 轴于
轴于![]() ,
,![]() 轴于
轴于![]() ,∴
,∴![]() ,
,
∵![]() 是等腰直角三角形,
是等腰直角三角形,
∴![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,
在![]() 和
和![]() 中,
中,
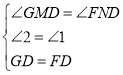 ,
,
∴![]() ,
,
∴![]() ,
,![]() ,设
,设![]() ,
,![]() ,
,
∵![]() 、
、![]() 在直线
在直线![]() 上,
上,
则:![]() ,
,![]() ,
,
解得:![]() ,
,![]() ,
,
![]() ,
,
∴![]() .
.
(3)如图,设![]() ,
,
∵![]() 轴,且点
轴,且点![]() 在直线
在直线![]() 上,
上,
∴![]() ,
,
∴![]() ,作
,作![]() 轴于
轴于![]() .
.
∴![]() ,
,
∴![]() ,
,
由勾股定理可知:![]() ,
,
∵四边形![]() 为菱形,
为菱形,
∴![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() .
.
∴![]() ,
,
∴![]() ,
,![]() ,
,
∵![]() ,
,![]() ,
,![]() ,
,
∴![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠BAC=90°,AB=AC.在平面内任取一点D,连结AD(AD<AB),将线段AD绕点A逆时针旋转90°,得到线段AE,连结DE,CE,BD.
(1)直线BD和CE的位置关系是 ;
(2)猜测BD和CE的数量关系并证明;
(3)设直线BD,CE交于点P,把△ADE绕点A旋转,当∠EAC=90°,AB=2,AD=1时,直接写出PB的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2020年新冠肺炎爆发,省疾控中心组织医护人员和防疫药品赶赴湖北救援,装载防疫药品的货运飞机从机场出发,以600千米/小时的速度飞行,半小时后医护人员乘坐客运飞机从同一个机场出发,客运飞机速度是货运飞机速度的1.2倍,结果客运飞机比装载防疫药品的货运飞机迟15分钟到达湖北.
(1)设货运飞机全程飞行时间为t小时,用t表示出发的机场到湖北的路程s;
(2)求出发的机场到湖北的路程.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知反比例函数y=![]() .
.
(1)若该反比例函数的图象与直线y=kx+4(k≠0)只有一个公共点,求k的值;
(2)如图,反比例函数y=![]() (1≤x≤4)的图象记为曲线C1,将C1向左平移2个单位长度,得曲线C2,请在图中画出C2,并直接写出C1平移到C2处所扫过的面积.
(1≤x≤4)的图象记为曲线C1,将C1向左平移2个单位长度,得曲线C2,请在图中画出C2,并直接写出C1平移到C2处所扫过的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx+c(a≠0对称轴为直线x=1,与x轴的一个交点坐标为(﹣1,0),其部分图象如图所示,下列结论:①abc<0;②4ac<b2;③方程ax2+bx+c=0的两个根是x1=﹣1,x2=3;④3a+c>0;⑤当y≥0时,x的取值范围是﹣1≤x≤3.其中结论正确的个数是( )
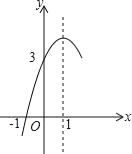
A. 1个B. 2个C. 3D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一艘轮船在![]() 处测得灯塔
处测得灯塔![]() 位于其北偏东
位于其北偏东![]() 方向上,轮船沿正东方向航行20海里到达
方向上,轮船沿正东方向航行20海里到达![]() 处后,测得灯塔
处后,测得灯塔![]() 位于其北偏东
位于其北偏东![]() 方向上,轮船沿计划路线航行时与灯塔
方向上,轮船沿计划路线航行时与灯塔![]() 的距离最少是_______海里.(结果保留根号)
的距离最少是_______海里.(结果保留根号)

查看答案和解析>>
科目:初中数学 来源: 题型:
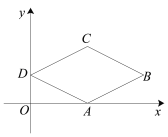
【题目】如图,已知在平面直角坐标系中,四边形ABCD是菱形,其中B点坐标是(8,2),D点坐标是(0,2),点A在x轴上,则菱形ABCD的周长是( )
A.2![]()
B.8
C.8![]()
D.12
查看答案和解析>>
科目:初中数学 来源: 题型:
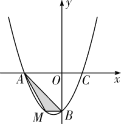
【题目】(2010河南23题)在平面直角坐标系中,已知抛物线经过![]() ,
,![]() ,
,![]() 三点.
三点.
(1)求抛物线的解析式;
(2)若点M为第三象限内抛物线上一动点,点M的横坐标为m,![]() 的面积为S.求S关于m的函数关系式,并求出S的最大值;
的面积为S.求S关于m的函数关系式,并求出S的最大值;
(3)若点P是抛物线上的动点,点Q是直线![]() 上的动点,判断有几个位置能使以点P、Q、B、O为顶点的四边形为平行四边形,直接写出相应的点Q的坐标.
上的动点,判断有几个位置能使以点P、Q、B、O为顶点的四边形为平行四边形,直接写出相应的点Q的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某水果连锁店销售某种热带水果,其进价为20元/千克.销售一段时间后发现:该水果的日销量![]() (千克)与售价
(千克)与售价![]() (元/千克)的函数关系如图所示:
(元/千克)的函数关系如图所示:
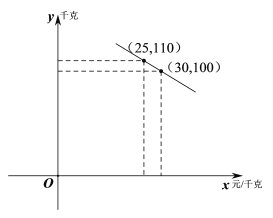
(1)求![]() 关于
关于![]() 的函数解析式;
的函数解析式;
(2)当售价为多少元/千克时,当日销售利润最大,最大利润为多少元?
(3)由于某种原因,该水果进价提高了![]() 元/千克(
元/千克(![]() ),物价局规定该水果的售价不得超过40元/千克,该连锁店在今后的销售中,日销售量与售价仍然满足(1)中的函数关系.若日销售最大利润是
),物价局规定该水果的售价不得超过40元/千克,该连锁店在今后的销售中,日销售量与售价仍然满足(1)中的函数关系.若日销售最大利润是![]() 元,请直接写出
元,请直接写出![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com