
【题目】四边形ABCD中,∠A=145°,∠D=75°.
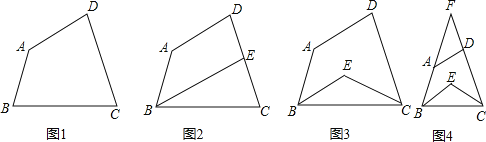
(1)如图1,若∠B=∠C,试求出∠C的度数;
(2)如图2,若∠ABC的角平分线BE交DC于点E,且BE∥AD,试求出∠C的度数;
(3)①如图3,若∠ABC和∠BCD的角平分线交于点E,试求出∠BEC的度数.
②在①的条件下,若延长BA、CD交于点F(如图4),将原来条件“∠A=145°,∠D=75°”改为“∠F=40°”,其他条件不变,∠BEC的度数会发生变化吗?若不变,请说明理由;若变化,求出∠BEC的度数.
【答案】(1)∠C=70°;(2)∠C=70°;(3)①∠BEC=110°;②不变.∠BEC=110°.
【解析】
(1)先根据四边形内角和等于360°求出∠B+∠C的度数,再除以2即可求解;
(2)先根据平行线的性质得到∠ABE的度数,再根据角平分线的定义得到∠ABC的度数,再根据四边形内角和等于360°求出∠BEC的度数;
(3)①先根据四边形内角和等于360°求出∠ABC+∠BCD的度数,再根据角平分线的定义得到∠EBC+∠ECB的度数,再根据三角形内角和等于180°求出∠BEC的度数;
②先根据三角形内角和等于180°求出∠FBC+∠BCF的度数,再根据角平分线的定义得到∠EBC+∠ECB的度数,再根据三角形内角和等于180°求出∠BEC的度数.
(1)∵四边形ABCD中,∠A=145°,∠D=75°,
∴∠B+∠C=360°-(145°+75°)=140°,
∵∠B=∠C,
∴∠C=70°;
(2)∵BE∥AD,
∴∠ABE=180°-∠A=180°-145°=35°,
∵∠ABC的角平分线BE交DC于点E,
∴∠ABC=70°,
∴∠C=360°-(145°+75°+70°)=70°;
(3)①∵四边形ABCD中,∠A=145°,∠D=75°,
∴∠B+∠C=360°-(145°+75°)=140°,
∵∠ABC和∠BCD的角平分线交于点E,
∴∠EBC+∠ECB=70°,
∴∠BEC=180°-70°=110°;
②不变.
∵∠F=40°,
∴∠FBC+∠BCF=180°-40°=140°,
∵∠ABC和∠BCD的角平分线交于点E,
∴∠EBC+∠ECB=70°,
∴∠BEC=180°-70°=110°.


科目:初中数学 来源: 题型:
【题目】如图1,二次函数y1=(x﹣2)(x﹣4)的图象与x轴交于A、B两点(点A在点B的左侧),其对称轴l与x轴交于点C,它的顶点为点D.
(1)写出点D的坐标 .
(2)点P在对称轴l上,位于点C上方,且CP=2CD,以P为顶点的二次函数y2=ax2+bx+c(a≠0)的图象过点A.
①试说明二次函数y2=ax2+bx+c(a≠0)的图象过点B;
②点R在二次函数y1=(x﹣2)(x﹣4)的图象上,到x轴的距离为d,当点R的坐标为 时,二次函数y2=ax2+bx+c(a≠0)的图象上有且只有三个点到x轴的距离等于2d;
③如图2,已知0<m<2,过点M(0,m)作x轴的平行线,分别交二次函数y1=(x﹣2)(x﹣4)y2=ax2+bx+c(a≠0)的图象于点E、F、G、H(点E、G在对称轴l左侧),过点H作x轴的垂线,垂足为点N,交二次函数y1=(x﹣2)(x﹣4)的图象于点Q,若△GHN∽△EHQ,求实数m的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着科技的发展,某快递公司为了提高分拣包裹的速度,使用机器人代替人工进行包裹分拣,若甲机器人工作![]() ,乙机器人工作
,乙机器人工作![]() ,一共可以分拣700件包裹;若甲机器人工作
,一共可以分拣700件包裹;若甲机器人工作![]() ,乙机器人工作
,乙机器人工作![]() ,一共可以分拣650件包裹.
,一共可以分拣650件包裹.
(1)求甲、乙两机器人每小时各分拣多少件包裹;
(2)去年“双十一”期间,快递公司的业务量猛增,为了让甲、乙两机器人每天分拣包裹的总数量不低于2250件,则它们每天至少要一起工作多少小时?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】尺规作图与图形变换
(尺规作图)(不写作法,保留作图痕迹)
如图,一辆汽车在直线形的公路上由点A向点B行驶,M,N 是分别位于公路两侧的村庄.
(1)在图1中求作一点P,使汽车行驶到此位置时,与村庄M,N的距离之和最小;

(2)在图2中求作一点Q,使汽车行驶到此位置时,与村庄 M,N 的距离相等.

(图形变换)
如图3所示,在正方形网格中,△ABC为格点三角形(即三角形的顶点都在格点上).
(3)把△ABC 沿 BA 方向平移后,点 A 移到点![]() ,请你在网格中画出平移后得到的
,请你在网格中画出平移后得到的![]() ;
;
(4)把![]() 绕点
绕点![]() 按逆时针方向旋转 90°,请你在网格中画出旋转后的
按逆时针方向旋转 90°,请你在网格中画出旋转后的![]() .
.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2016年3月国际风筝节期间,王大伯决定销售一批风筝,经市场调研:蝙蝠型风筝进价每个为10元,当售价每个为12元时,销售量为180个,若售价每提高1元,销售量就会减少10个,请回答以下问题:
(1)用表达式表示蝙蝠型风筝销售量y(个)与售价x(元)之间的函数关系(12≤x≤30);
(2)王大伯为了让利给顾客,并同时获得840元利润,售价应定为多少?
(3)当售价定为多少时,王大伯获得利润W最大,最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,菱形纸片ABCD中,∠A=60°,折叠菱形纸片ABCD,使点C落在DP(P为AB的中点)所在的直线上,得到经过点D的折痕DE,若菱形边长为1,则点E到CD的距离为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图,已知直线a∥b,点A在直线a上,点B. C在直线b上,点P在线段AB上,∠1=70,∠2=100,求∠PCB的度数.

(2)下表是某商行一种商品的销售情况,该商品原价为560元,随着不同幅度的降价(单位:元),日销量(单位:件)发生相应变化如下表:
降价 | 5 | 10 | 15 | 20 | 25 | 30 | 35 |
日销量 | 78 | 81 | 84 | 87 | 90 | 93 | 96 |
①根据表格所列出的变化关系,请你估计降价之前的日销量是多少件?
②根据表格所列出的变化关系,请直接写出![]() 与
与![]() 的关系式.
的关系式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,正比例函数y=ax的图象与反比例函数y=![]() 的图象交于点A(3,2)
的图象交于点A(3,2)
(1)试确定上述正比例函数和反比例函数的表达式;
(2)根据图象回答,在第一象限内,当x取何值时,反比例函数的值大于正比例函数的值?
(3)点M(m,n)是反比例函数图象上的一动点,其中0<m<3,过点M作直线MB∥x轴,交y轴于点B;过点A作直线AC∥y轴交x轴于点C,交直线MB于点D.当四边形OADM的面积为6时,请判断线段BM与DM的大小关系,并说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com