
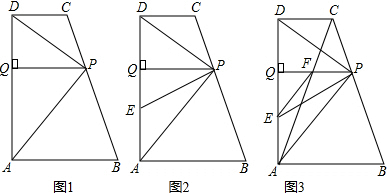
 如图,若O为EH的中点,要使△EOF≌△HOG,不能加什么条件( )
如图,若O为EH的中点,要使△EOF≌△HOG,不能加什么条件( )| A. | FO=GO | B. | AB∥CD | C. | ∠AFG=∠FGD | D. | EF=GH |
分析 根据全等三角形的判定定理进行判断并作出正确的选择.
解答  解:如图,∵O为EH的中点,且∠EOF=∠HPG(对顶角相等).
解:如图,∵O为EH的中点,且∠EOF=∠HPG(对顶角相等).
∴OE=OH.
即在△EOF与△HOG中,已知一组对应角和一组对应边相等.
A、若FO=GO时,利用SAS可以判定△EOF≌△HOG,故本选项错误;
B、若AB∥CD时,可以判定∠FEO=∠GHO,利用ASA可以判定△EOF≌△HOG,故本选项错误;
C、若∠AFG=∠FGD时,利用ASA可以判定△EOF≌△HOG,故本选项错误;
D、若EF=GH时,利用SSA不可以判定△EOF≌△HOG,故本选项正确;
故选:D.
点评 本题考查了全等三角形的判定.注意:AAA、SSA不能判定两个三角形全等,判定两个三角形全等时,必须有边的参与,若有两边一角对应相等时,角必须是两边的夹角.


 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案科目:初中数学 来源: 题型:解答题
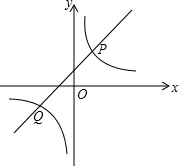 如图,直线y=k1x+1与双曲线y=$\frac{{k}_{2}}{x}$相交于P(1,m),Q(-2,-1)两点;
如图,直线y=k1x+1与双曲线y=$\frac{{k}_{2}}{x}$相交于P(1,m),Q(-2,-1)两点;查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
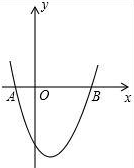 如图,抛物线y=x2-x-2交x轴于A(-1,0),B两点,交y轴于C(0,-2),过A,C画直线.点M在抛物线上,以M为圆心的圆与直线AC相切,切点为H,若⊙M的半径为$\frac{4\sqrt{5}}{5}$,求点M的坐标.
如图,抛物线y=x2-x-2交x轴于A(-1,0),B两点,交y轴于C(0,-2),过A,C画直线.点M在抛物线上,以M为圆心的圆与直线AC相切,切点为H,若⊙M的半径为$\frac{4\sqrt{5}}{5}$,求点M的坐标.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
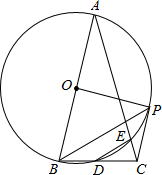 如图,在△ABC中,AB=AC,∠A=30°,以AB为直径的⊙O交BC于点D,交AC于点E,过点B作∠DBP=30°,交⊙O于点P,连接DE、CP、OP.
如图,在△ABC中,AB=AC,∠A=30°,以AB为直径的⊙O交BC于点D,交AC于点E,过点B作∠DBP=30°,交⊙O于点P,连接DE、CP、OP.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
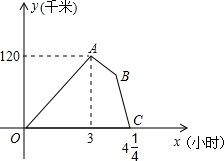 某物流公司的快递车和货车同时从甲地出发,以各自的速度匀速向乙地行驶,快递车到达乙地后卸完物品再另装货物共用45分钟,立即按原路以另一速度匀速返回,直至与货车相遇.已知货车的速度为60千米/时,两车之间的距离y(千米)与货车行驶时间x(小时)之间的函数图象如图所示.
某物流公司的快递车和货车同时从甲地出发,以各自的速度匀速向乙地行驶,快递车到达乙地后卸完物品再另装货物共用45分钟,立即按原路以另一速度匀速返回,直至与货车相遇.已知货车的速度为60千米/时,两车之间的距离y(千米)与货车行驶时间x(小时)之间的函数图象如图所示.查看答案和解析>>
科目:初中数学 来源: 题型:选择题

| A. | 780 | B. | 800 | C. | 820 | D. | 840 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com