
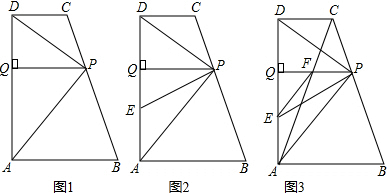
分析 (1)由等边对等角可得:∠1=∠2,∠3=∠4,然后由三角形内角和定理及平行线的性质可得:∠2+∠3=90°,然后由平角的定义可得:∠DPA=90°,进而可得DP⊥AP;
(2)分别过点C与点P作CH⊥AB,PG⊥AB,垂足分别为:H、G,可得:四边形AHDC是矩形,四边形QAGP是矩形,进而可得:DC=AH,AD=CH,PG=AQ,然后由AB=2CD=2,可得CP=CD=1,BP=AB=2,AH=1,BH=1,BC=3,在Rt△BCH中,由勾股定理得:CH=2$\sqrt{2}$,进而可求AD=CH=2$\sqrt{2}$,然后由CH⊥AB,PG⊥AB,可得△BPG∽△BCH,然后由相似三角形的对应边成比例,可求PG=$\frac{4\sqrt{2}}{3}$,进而可求AQ=$\frac{4\sqrt{2}}{3}$,然后由∠DPA=90°,E为AD的中点,根据直角三角形斜边的中线等于斜边的一半,可得EP=$\frac{1}{2}AD$=DE=AE=$\sqrt{2}$,进而可求QE=$\frac{\sqrt{2}}{3}$,在Rt△PQE中,由勾股定理得:PQ=$\frac{4}{3}$,然后根据三角函数的定义可求tan∠PED=$\frac{PQ}{QE}=2\sqrt{2}$;
(3)延长AP与DC的延长线交于点G,由CD=CP,BA=BP,PQ∥DC∥AB,可得:∠BAP=∠BPA=∠APQ=∠CPG=∠G,进而可得:CP=CG=DC,然后由PQ∥DC,根据平行线分线段成比例定理可得:$\frac{QF}{DC}=\frac{AF}{AC}=\frac{PF}{GC}$,进而可得:QF=PF,然后由tan∠FEQ=2:3,即$\frac{QF}{QE}=\frac{2}{3}$,设QF=2x,则QE=3x,QP=4x,然后由射影定理得:DQ•AQ=PQ2,进而将AQ与DQ用x表示,由DC∥QP∥AB,根据平行线分线段成比例定理可得:$\frac{AB}{DC}=\frac{BP}{CP}=\frac{AQ}{DQ}=\frac{8x}{2x}=4$.
解答 解:(1)如图1,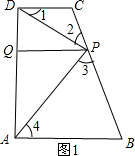
∵PC=DC,PB=AB,
∴∠1=∠2,∠3=∠4,
∵∠1+∠2+∠C=180°,∠3+∠4+∠B=180°,
∴2∠2+2∠3+∠C+∠B=360°,
∵AB∥CD,
∴∠C+∠B=180°,
∴2∠2+2∠3=180°,
∴∠2+∠3=90°,
∵∠2+∠3+∠DPA=180°,
∴∠DPA=90°,
∴DP⊥AP;
(2)分别过点C与点P作CH⊥AB,PG⊥AB,垂足分别为:H、G,如图2,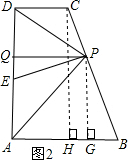
可得:四边形AHDC是矩形,四边形QAGP是矩形,
∴DC=AH,AD=CH,PG=AQ,
∵AB=2CD=2,
∴CP=CD=1,BP=AB=2,
∴AH=1,BH=AB-AH=1,BC=CP+BP=1+2=3,
在Rt△BCH中,由勾股定理得:CH=$\sqrt{B{C}^{2}-H{B}^{2}}$=$\sqrt{8}$=$2\sqrt{2}$,
∴AD=CH=2$\sqrt{2}$,
∵CH⊥AB,PG⊥AB,
∴PG∥CH,
∴△BPG∽△BCH,
∴$\frac{PG}{CH}=\frac{BP}{BC}$,
即:$\frac{PG}{2\sqrt{2}}=\frac{2}{3}$,
∴PG=$\frac{4\sqrt{2}}{3}$,
∴AQ=$\frac{4\sqrt{2}}{3}$,
∵∠DPA=90°,E为AD的中点,
∴EP=$\frac{1}{2}AD$=DE=AE=$\sqrt{2}$,
∴QE=AQ-AE=$\frac{\sqrt{2}}{3}$,
在Rt△PQE中,由勾股定理得:
PQ=$\sqrt{P{E}^{2}-Q{E}^{2}}$=$\frac{4}{3}$,
∴tan∠PED=$\frac{PQ}{QE}=2\sqrt{2}$;
(3)延长AP与DC的延长线交于点G,如图3,
∵CD=CP,BA=BP,PQ∥DC∥AB,
∴∠CDP=∠CPD=∠DPQ,∠BAP=∠BPA=∠APQ=∠CPG=∠G,
∴2∠DPQ+2∠APQ=180°,CP=CG,
∴∠DPA=90°,DC=CG,
∵PQ∥DC,
∴$\frac{QF}{DC}=\frac{AF}{AC}=\frac{PF}{GC}$,
∴QF=PF,
在Rt△EQF中,
∵tan∠FEQ=2:3,
即$\frac{QF}{QE}=\frac{2}{3}$,
∴设QF=2x,则QE=3x,QP=4x,
∵∠APD=∠DQP=90°,
由射影定理得:DQ•AQ=PQ2,
∴(DE-3x)(AE+3x)=(4x)2,
∵AE=DE,
∴DE2-9x2=16x2,
∴DE=5x,
∴DQ=DE-EQ=2x,
AQ=AE+QE=DE+QE=8x,
∵DC∥QP∥AB,
∴$\frac{AB}{DC}=\frac{BP}{CP}=\frac{AQ}{DQ}=\frac{8x}{2x}=4$.
∴当$\frac{AB}{DC}$=4时,tan∠FEQ=$\frac{2}{3}$.
故答案为:4.
点评 此题是四边形的综合题型,主要考查了直角梯形的性质,直角三角形的性质,等腰三角形的性质,相似三角形的判定与性质等知识点,解题的关键是:适当的添加辅助线,借助平行线的性质解决问题.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
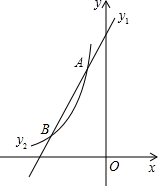 如图,已知一次函数y1=2x-3k的图象与反比例函数y2=$\frac{k-2}{x}$(x<0)的图象在第二象限内相交于A、B两点,其中点A的纵坐标为4.
如图,已知一次函数y1=2x-3k的图象与反比例函数y2=$\frac{k-2}{x}$(x<0)的图象在第二象限内相交于A、B两点,其中点A的纵坐标为4.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
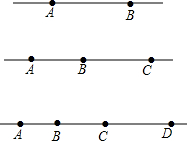 在一条直线上取两点A,B共得几条线段?在一条直线上取三个点A,B,C,共得几条线段?在一条直线上取A,B,C,D四个点时,共得多少条线段?在一条直线上取n个点时,共可得多少条线段?若将此题中直线上由点变为线段,结论有何变化?
在一条直线上取两点A,B共得几条线段?在一条直线上取三个点A,B,C,共得几条线段?在一条直线上取A,B,C,D四个点时,共得多少条线段?在一条直线上取n个点时,共可得多少条线段?若将此题中直线上由点变为线段,结论有何变化?查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在△ABC中,AB=AC,以AB为直径的半圆⊙O交BC于点D,DE⊥AC,垂足为点E.
如图,在△ABC中,AB=AC,以AB为直径的半圆⊙O交BC于点D,DE⊥AC,垂足为点E.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
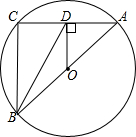 如图,AB是⊙O的直径,AC是⊙O的弦,作0D⊥AC,垂足为点D,连接BD.若AB=5cm,AC=4cm,则BD的长为$\sqrt{13}$.
如图,AB是⊙O的直径,AC是⊙O的弦,作0D⊥AC,垂足为点D,连接BD.若AB=5cm,AC=4cm,则BD的长为$\sqrt{13}$.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | “任意一个三角形的外角和是180度”这一事件是不可能事件 | |
| B. | 一组数据1,6,3,9,8,5的中位数是6 | |
| C. | “面积相等的两个三角形全等”是必然事件 | |
| D. | 必然事件发生的概率为0 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com