
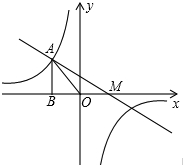
 如图,点A(-2,b)是函数y=$\frac{k}{x}$的图象上的点,过点A作AB⊥x轴于点B,△AOB的面积为2,若一次函数y=ax+1的图象经过点A且与x轴交于点M,则AO:AM=$\sqrt{2}$:$\sqrt{5}$.
如图,点A(-2,b)是函数y=$\frac{k}{x}$的图象上的点,过点A作AB⊥x轴于点B,△AOB的面积为2,若一次函数y=ax+1的图象经过点A且与x轴交于点M,则AO:AM=$\sqrt{2}$:$\sqrt{5}$. 分析 由△AOB的面积为2可求出反比例函数和A点坐标,可求得反比例函数解析式和A点坐标,再代入一次函数解析式可求得一次函数解析式中的a,求得一次函数的解析式,再令y=0可求出M点的坐标,在Rt△ABM中利用勾股定理可求得AM,且容易求得OA,可求得答案.
解答 解:∵△AOB的面积为2,A(-2,b),
∴$\frac{1}{2}$OB•AB=$\frac{1}{2}$×2b=2,解得b=2,
∴A点坐标为(-2,2),
∴k=-2×2=-4,
∴反比例函数为y=-$\frac{4}{x}$,
又A点在一次函数y=ax+1的图象上,
∴2=-2a+1,解得a=-$\frac{1}{2}$,
∴一次函数解析式为y=-$\frac{1}{2}$x+1,
令y=0,即-$\frac{1}{2}$x+1=0,解得x=2,
∴M点坐标为(2,0),
在Rt△ABM中,AB=2,BM=BO+OM=2+2=4,
由勾股定理可得AM=$\sqrt{A{B}^{2}+B{M}^{2}}$=$\sqrt{{2}^{2}+{4}^{2}}$=2$\sqrt{5}$,
且在Rt△AOB中可求得OA=2$\sqrt{2}$,
∴AO:AM=2$\sqrt{2}$:2$\sqrt{5}$=$\sqrt{2}$:$\sqrt{5}$,
故答案为:$\sqrt{2}$:$\sqrt{5}$.
点评 本题主要考查待定系数法求函数解析式及函数的交点的求法,由三角形的面积求得反比例函数的解析式是解题的关键.


 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
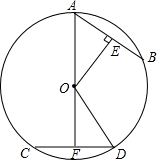 如图,⊙O中弦AB与弦CD相等,过点O分别作OE,OF垂直AB,CD于E,F点,连接AO,OD.将Rt△AOE绕O点顺时针旋转一定的角α,△AOE与△DOF能够重合吗?说明理由.
如图,⊙O中弦AB与弦CD相等,过点O分别作OE,OF垂直AB,CD于E,F点,连接AO,OD.将Rt△AOE绕O点顺时针旋转一定的角α,△AOE与△DOF能够重合吗?说明理由.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com