
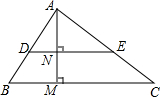
 如图,已知△ADE∽△ABC,且AD=3,BD=2.若AM⊥BC于M,AM交DE于N,AM=4,则AN=$\frac{12}{5}$.
如图,已知△ADE∽△ABC,且AD=3,BD=2.若AM⊥BC于M,AM交DE于N,AM=4,则AN=$\frac{12}{5}$.  优生乐园系列答案
优生乐园系列答案科目:初中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
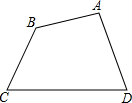 如图,四边形ABCD,某图形设计要求把该四边形改设计成一个平行四边形且面积扩大为原来的2倍,A、B、C、D这四点必须在新的平行四边形的四条边上.你能给出一种符合要求的设计方案吗?
如图,四边形ABCD,某图形设计要求把该四边形改设计成一个平行四边形且面积扩大为原来的2倍,A、B、C、D这四点必须在新的平行四边形的四条边上.你能给出一种符合要求的设计方案吗?查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,已知:点E是正方形ABCD的BC边上的点,现将△DCE沿折痕DE向上翻折,使DC落在对角线DB上,则CD:CE==($\sqrt{2}$+1):1.
如图,已知:点E是正方形ABCD的BC边上的点,现将△DCE沿折痕DE向上翻折,使DC落在对角线DB上,则CD:CE==($\sqrt{2}$+1):1.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com