
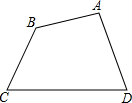
 如图,四边形ABCD,某图形设计要求把该四边形改设计成一个平行四边形且面积扩大为原来的2倍,A、B、C、D这四点必须在新的平行四边形的四条边上.你能给出一种符合要求的设计方案吗?
如图,四边形ABCD,某图形设计要求把该四边形改设计成一个平行四边形且面积扩大为原来的2倍,A、B、C、D这四点必须在新的平行四边形的四条边上.你能给出一种符合要求的设计方案吗? 分析 根据平行四边形的性质,平行四边形的对角线把平行四边形分成面积相等两部分.
解答 解: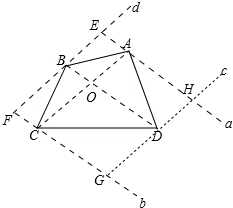 分别过A、C两点作直线a∥BD,直线b∥BD,分别过B、D作直线c∥AC,直线d∥AC,
分别过A、C两点作直线a∥BD,直线b∥BD,分别过B、D作直线c∥AC,直线d∥AC,
直线a和直线c、d交于点H、E,直线b和直线c、d交于点G、F,
四边形EFGH就是所求作的四边形.
∵四边形EBOA是平行四边形,
∴S△ABE=S△ABO,同理:S△BCF=S△BCO,S△CDG=S△CDO,S△AHD=S△AOD,
∴S四边形EFGH=2•S四边形ABCD.
点评 本题考查平行四边形的性质、作图-应用与设计,解题的关键是灵活运用平行四边形的性质,平行四边形的对角线把四边形分成面积相等的两部分.


科目:初中数学 来源: 题型:解答题
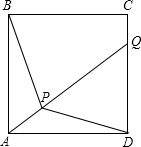 如图,点P是正方形ABCD内一点,并延长AP与DC相交于点Q.
如图,点P是正方形ABCD内一点,并延长AP与DC相交于点Q.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
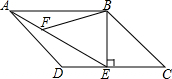 如图,已知在?ABCD中,过点B作BE⊥CD于点E,连接AE,F是AE上的点,且∠BFE=∠C.
如图,已知在?ABCD中,过点B作BE⊥CD于点E,连接AE,F是AE上的点,且∠BFE=∠C.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{1}{a+5}$ | B. | $\frac{1}{a-5}$ | C. | $\frac{a+5}{a(a-5)}$ | D. | $\frac{1}{a}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com