
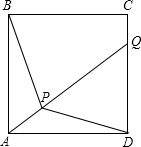
 如图,点P是正方形ABCD内一点,并延长AP与DC相交于点Q.
如图,点P是正方形ABCD内一点,并延长AP与DC相交于点Q.分析 (1)如图1中,将△PAD绕点A逆时针旋转90°得△EAB,利用勾股定理逆定理证明∠PEB=90°,求出∠BEA即可解决问题.
(2)如图2中,将△ABP绕点B顺时针旋转60°得△EBQ,连接PQ,AE,作EF⊥DA交DA的延长线于F,当E、Q、P、D四点共线时,PA+PB+PD最小,设正方形边长为a,在RT△EFD中利用勾股定理列出方程即可解决问题.
解答 解:(1)如图1中, 将△PAD绕点A逆时针旋转90°得△EAB,
将△PAD绕点A逆时针旋转90°得△EAB,
∵PA=AE=$\sqrt{2}$,∠EAP=90°,BE=PD=$\sqrt{5}$,PB=3,
∴PE=$\sqrt{A{E}^{2}+A{P}^{2}}$=$\sqrt{(\sqrt{2})^{2}+(\sqrt{2})^{2}}$=2,
∴BE2+PE2=5+4=9.PB2=32=9,
∴PB2=BE2+PE2,
∴∠PEB=90°,
∵∠AEP=∠APE=45°,
∴∠APD=∠AEB=45°+90°=135°,
∴∠DPQ=180°-∠APD=45°.
(2)如图2中,将△ABP绕点B顺时针旋转60°得△EBQ,连接PQ,AE,作EF⊥DA交DA的延长线于F.
当E、Q、P、D四点共线时,PA+PB+PD最小,这个最小值就是线段ED的长.
∴DE=$\sqrt{6}$+$\sqrt{2}$,
∵BE=BA,∠ABE=60°,
∴△ABE是等边三角形,∠EAB=60°,
∴AE=AB=AD,∠EAD=150°,∠EAF=30°设正方形边长为a,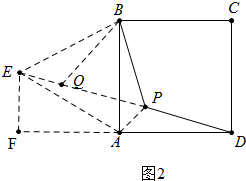
在RT△AEF中,∵∠F=90°,AE=a,∠EAF=30°,
∴EF=$\frac{1}{2}$a,AF=$\frac{\sqrt{3}}{2}$a,
在RT△EFD中,∵EF2+FD2=ED2,
∴($\frac{1}{2}$a)2+(a+$\frac{\sqrt{3}}{2}$a)2=($\sqrt{6}$+$\sqrt{2}$)2,
∴a2=4,
∵a>0,
∴a=2,
∴正方形ABCD边长为2.
点评 本题考查轴对称-最短问题、正方形的性质、勾股定理等知识,解题的关键是利用旋转构造全等三角形,学会添加辅助线的方法,属于中考常考题型.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,要在河边修建一个水泵站,分别向A村、B村送水,已知:A、B到直线l的距离分别是1km和3km,两点的水平距离为3km,要在直线l上找到一个点P,使PA+PB得和最小,请在图中找出点P的位置,并计算PA+PB的最小值.
如图,要在河边修建一个水泵站,分别向A村、B村送水,已知:A、B到直线l的距离分别是1km和3km,两点的水平距离为3km,要在直线l上找到一个点P,使PA+PB得和最小,请在图中找出点P的位置,并计算PA+PB的最小值.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | -x5+y3 | B. | 3x3+x+1 | C. | 2ab+cd+2 | D. | a4+3a3+2ab2+b3 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
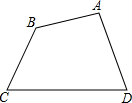 如图,四边形ABCD,某图形设计要求把该四边形改设计成一个平行四边形且面积扩大为原来的2倍,A、B、C、D这四点必须在新的平行四边形的四条边上.你能给出一种符合要求的设计方案吗?
如图,四边形ABCD,某图形设计要求把该四边形改设计成一个平行四边形且面积扩大为原来的2倍,A、B、C、D这四点必须在新的平行四边形的四条边上.你能给出一种符合要求的设计方案吗?查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com