
【题目】已知直线l1:y=﹣2x+5和直线l2:y=x﹣4,直线l1与y轴交于点A,直线l2与y轴交于点B.

(1)求两条直线l1和l2的交点C的坐标;
(2)求两条直线与y轴围成的三角形的面积;
(3)已知点D是y轴上一点,若△BCD为等腰直角三角形,直接写出D点坐标.
【答案】(1)(3,﹣1);(2)![]() ;(3) (0,﹣1)或(0,2)
;(3) (0,﹣1)或(0,2)
【解析】
(1)解方程组即可得到两条直线l1和l2的交点C的坐标;
(2)根据点C为(3,﹣1),直线l1和l2与y轴的交点分别为A(0,5)、B(0,﹣4),即可得到两条直线与y轴围成的三角形的面积;
(3)分两种情况,根据函数图像及等腰直角三角形的特点即可求解.
解:(1)由题意得![]() ,
,
解方程组得![]()
∴l1和l2的交点C为(3,﹣1);
(2)如图,过点C作CE⊥y轴于E,则CE=3.
在y=﹣2x+5中,令x=0,则y=5,
在y=x﹣4中,令x=0,则y=﹣4,
∴直线l1和l2与y轴的交点分别为A(0,5)、B(0,﹣4),
则![]() =
=![]() =
=![]() =
=![]() ;
;
(3)分两种情况讨论:当∠BDC=90°时,点D与点E重合,即D(0,﹣1);
当∠BCD=90°时,BE=DE=3,DO=3﹣1=2,即D(0,2);
∴D点坐标为(0,﹣1)或(0,2).



科目:初中数学 来源: 题型:
【题目】如图,已知AB是圆O的直径,弦CD⊥AB,垂足为H,与AC平行的圆O的一条切线交CD的延长线于点M,交AB的延长线于点E,切点为F,连接AF交CD于点N.
(1)求证:CA=CN;
(2)连接DF,若cos∠DFA=![]() ,AN=
,AN=![]() ,求圆O的直径的长度.
,求圆O的直径的长度.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商品的进价为每件50元,售价为每件60元,每天可卖出190件;如果每件商品的售价每上涨1元,则每天少卖10件,设每件商品的售价上涨x元(x为正整数),每天的销售利润为y元.
(1)求y关于x的关系式;
(2)每件商品的售价定为多少元时,每天的利润恰为1980元?
(3)每件商品的售价定为多少元时,每天可获得最大利润?最大利润是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某游泳馆每年夏季推出两种游泳付费方式,方式一:先购买会员证,每张会员证100元,只限本人当年使用,凭证游泳每次再付费5元;方式二:不购买会员证,每次游泳付费9元.
设小明计划今年夏季游泳次数为x(x为正整数).
(I)根据题意,填写下表:
游泳次数 | 10 | 15 | 20 | … | x |
方式一的总费用(元) | 150 | 175 | ______ | … | ______ |
方式二的总费用(元) | 90 | 135 | ______ | … | ______ |
(Ⅱ)若小明计划今年夏季游泳的总费用为270元,选择哪种付费方式,他游泳的次数比较多?
(Ⅲ)当x>20时,小明选择哪种付费方式更合算?并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们知道对于x轴上的任意两点A(x1,0),B(x2,0),有AB=|x1﹣x2|,而对于平面直角坐标系中的任意两点P1(x1,y1),P2(x2,y2),我们把|x1﹣x2|+|y1﹣y2|称为Pl,P2两点间的直角距离,记作d(P1,P2),即d(P1,P2)=|x1﹣x2|+|y1﹣y2|.
(1)已知O为坐标原点,若点P坐标为(1,3),则d(O,P)= ;
(2)已知O为坐标原点,动点P(x,y)满足d(O,P)=2,请写出x与y之间满足的关系式,并在所给的直角坐标系中画出所有符合条件的点P所组成的图形;
(3)试求点M(2,3)到直线y=x+2的最小直角距离.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,A是∠MON边OM上一点,AE∥ON.

(1)在图中作∠MON的角平分线OB(要求用尺规),交AE于点B;过点A画OB的垂线,垂足为点D,交ON于点C,连接CB,将图形补充完整.
(2)判断四边形OABC的形状,并证明你的结论.
解:四边形OABC是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2016年9月,某手机公司发布了新款智能手机,为了调查某小区业主对该款手机的购买意向,该公司在某小区随机对部分业主进行了问卷调查,规定每人只能从A类(立刻去抢购)、B类(降价后再去买)、C类(犹豫中)、D类(肯定不买)这四类中选一类,并制成了以下两幅不完整的统计图,由图中所给出的信息解答下列问题:
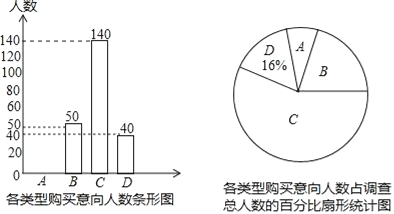
(1)扇形统计图中B类对应的百分比为 %,请补全条形统计图;
(2)若该小区共有4000人,请你估计该小区大约有多少人立刻去抢购该款手机.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面材料:
小明遇到这样一个问题:如图1,在△ABC中,DE∥BC分别交AB于D,交AC于E.已知CD⊥BE,CD=3,BE=4,求BC+DE的值.
小明发现,过点E作EF∥DC,交BC延长线于点F,构造△BEF,经过推理和计算能够使问题得到解决(如图2).

(1)请按照上述思路完成小明遇到的这个问题
(2)参考小明思考问题的方法,解决问题:
如图3,已知ABCD和矩形ABEF,AC与DF交于点G,AC=BF=DF,求∠DGC的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,长青化工厂与A、B两地有公路、铁路相连.这家工厂从A地购买一批每吨1000元的原料运回工厂,制成每吨8000元的产品运到B地.已知公路运价为1.5元/(吨·千米),铁路运价为1.2元/(吨·千米),且这两次运输共支出公路运输费15000元,铁路运输费97200元.

求:(1)该工厂从A地购买了多少吨原料?制成运往B地的产品多少吨?
(2)这批产品的销售款比原料费与运输费的和多多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com