
����Ŀ����ͼ��ֱ��y=��![]() x+6�ֱ�x�ᡢy����A��B���㣬������y=��
x+6�ֱ�x�ᡢy����A��B���㣬������y=��![]() x2+8����y�ύ�ڵ�D����P���������ڵ�һ�������ϵ�һ���㣬����P��PC��x���ڵ�C��
x2+8����y�ύ�ڵ�D����P���������ڵ�һ�������ϵ�һ���㣬����P��PC��x���ڵ�C��

��1����A������Ϊ ����D������Ϊ ��
��2��̽�����֣�
�ټ���P���D�غϣ���PB+PC= ����ֱ����д�𰸣�
�����жϣ���������һ��P��PB+PC��ֵ�Ƿ�Ϊ��ֵ����˵�����ɣ�
��3�����ж���PAB������Ƿ�������ֵ�������ڣ�������ֵ���������ʱ��P�����ꣻ�������ڣ�˵�����ɣ�
���𰸡���1����4��0������0��8������2����PB+PC=10�����ǣ���������3����PAB������������ֵ�������ֵΪ13����ʱ��P������Ϊ��6��![]() ��
��
��������
�����������1�������Ա����뺯��ֵ�Ķ�Ӧ��ϵ���ɵô𰸣�
��2���ٸ����߶εĺͲ�ɵ�PB���ɵô𰸣�
�ڸ��ݹ��ɶ������ɵ�PB�ij��������߶κͲ�ɵô𰸣�
��3����������ĺͲ�ɵö��κ��������ݶ��κ��������ʣ��ɵ����ֵ�������Ա����뺯��ֵ�Ķ�Ӧ��ϵ���ɵô𰸣�
�⣺��1��y=��![]() x+6��y=0ʱ��x=4����A��4��0����
x+6��y=0ʱ��x=4����A��4��0����
y=��![]() x2+8��x=0ʱ��y=8����D�����꣨0��8����
x2+8��x=0ʱ��y=8����D�����꣨0��8����
�ʴ�Ϊ����4��0������0��8����
��2����PB=PO��OB=8��6=2��PB+PC=8+2=10��
���ǣ��������£�
����P��PQ��y���ڵ�Q��
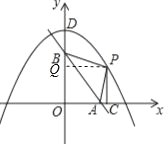
��P���������ϣ����ڵ�һ���ޣ�
����P��������x����![]() x2+8����
x2+8����
��PQ=x��PC=��![]() x2+8��
x2+8��
��4��x��8ʱ��PB=![]() =
=![]() =
=![]() x2+2��
x2+2��
��PB+PC=![]() x2+2+����
x2+2+����![]() x2��+8=10��
x2��+8=10��
��0��x��4ʱ��ͬ���ɵã�
��3�����ڣ�
����PAB�����ΪS��
�ɣ�2�����裮
��4��x��8ʱ����S=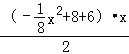 ��
��![]() ��
��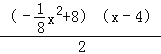
=��![]() x2+3x+4=��
x2+3x+4=��![]() ��x��6��2+13��
��x��6��2+13��
��0��x��4ʱ��s=��![]() ��x��6��2+13��
��x��6��2+13��
��x=6ʱ��S���=13��y=��![]() ��36+8=
��36+8=![]() ��
��
���PAB������������ֵ�������ֵΪ13����ʱ��P������Ϊ��6��![]() ��
��


 �����ҵ���������ϵ�д�
�����ҵ���������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���з��̻����Ӧ���⣺
���������ҹ����������Ͻ����ƶȣ��ס������˼ƻ�����ͬ�������ֱ�������ϱ��ս�15��Ԫ��10��Ԫ���ƻ�����ÿ���������ϱ��ս�0.2��Ԫ����ס������˼ƻ�ÿ��ֱ�������ϱ��ս������Ԫ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������ABCD�У���DAB=��B=��C=��D=90����AD=BC=8��AB=CD=17����EΪ����DC�ϵ�һ�����㣬��ADE����AD��E����ֱ��AE�Գƣ�����AD��BΪֱ��������ʱ��DE�ij�Ϊ ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��ABC����a��b��c���㣨a��b��2+|b��c|=0������ABC����״��_______��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪CΪ�߶�AB���е㣬DΪ�߶�AC���е㣮
��1��������Ӧ��ͼ�Σ����ͼ���߶ε�������д����Ӧ���߶Σ�
��2����ͼ�������߶εij��Ⱥ�Ϊ26�����߶�AC�ij��ȣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������һ���ر�����������壨����ͼ���������Ϲ����������ĵ���֮������7�������ķ�ͼ�п����۳ɷ��Ϲ�������ӵ��ǣ� ��
![]()
A�� B��
B�� C��
C�� D��
D��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABC�У���BAC=90����AB=3��AC=4��ADƽ����BAC��BC��D����BD�ij�Ϊ ��

�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com