
【题目】聪明好学的亮亮看到一课外书上有个重要补充:
(角平分线定理)三角形一个内角的平分线分对边所成的两条线段与这个角的两邻边对应成比例.于是他就和其他同学研究一番,写出了已知、求证如下:
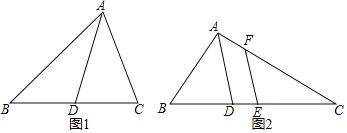
“已知:如图1,△ABC中,AD平分∠BAC交BC于点D,求证:![]() ”
”
可是他们依然找不到证明的方法,于是,老师提示:过点B作BE∥AC交AD延长线于点E,于是得到△BDE∽△CDA,从而打开思路.
(Ⅰ)请你按老师的提示或你认为其他可行的方法帮亮亮完成证明.
(Ⅱ)利用角平分线定理解决如下问题:
如图2,△ABC中,E是BC中点,AD是∠BAC的平分线,EF∥AD交AC于F,AB=7,AC=15,求AF的长.
科目:初中数学 来源: 题型:
【题目】下面是小元设计的“过圆上一点作圆的切线”的尺规作图过程.
已知:如图,⊙O及⊙O上一点P.
求作:过点P的⊙O的切线.


作法:如图,
①作射线OP;
②在直线OP外任取一点A,以点A为圆心,AP为半径作⊙A,与射线OP交于另一点B;
③连接并延长BA与⊙A交于点C;
④作直线PC;
则直线PC即为所求.
根据小元设计的尺规作图过程,
(1)使用直尺和圆规,补全图形;(保留作图痕迹)
(2)完成下面的证明:
证明:∵ BC是⊙A的直径,
∴∠BPC=90°(____________)(填推理的依据).
∴OP⊥PC.
又∵OP是⊙O的半径,
∴PC是⊙O的切线(____________)(填推理的依据).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD中,M为BC上一点,ME⊥AM,ME交CD于点F,交AD的延长线于点E,若AB=4,BM=2,则△DEF的面积为( )

A.9B.8C.15D.14.5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线AB表达式为y=﹣2x+2,交x轴于点A,交y轴于点B.若y轴负半轴上有一点C,且CO=![]() AO.
AO.
(1)求点C的坐标和直线AC的表达式;
(2)在直线AC上是否存在点D,使以点A、B、D为顶点的三角形与△ABO相似?若存在,请求出点D的坐标;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,对角线AC的垂直平分线EF分别交BC,AD于点E,F,若BE=3,AF=5,则AC的长为( )

A. ![]() B.
B. ![]() C. 10D. 8
C. 10D. 8
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,点E是BC的中点,连接DE,过点A作AG⊥ED交DE于点F,交CD于点G.
(1)若BC=4,求AG的长;
(2)连接BF,求证:AB=FB.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知正比例函数y=x的图象与反比例函数y=![]() (k为常数,且k≠0)的图象有一个交点的纵坐标是2.
(k为常数,且k≠0)的图象有一个交点的纵坐标是2.
(Ⅰ)当x=4时,求反比例函数y=![]() 的值;
的值;
(Ⅱ)当﹣2<x<﹣1时,求反比例函数y=![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
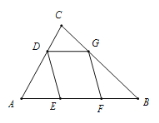
【题目】如图,在![]() 中,
中,![]() ,AB=5,BC=4,点D为边AC上的动点,作菱形DEFG,使点E、F在边AB上,点G在边BC上.若这样的菱形能作出两个,则AD的取值范围是( )
,AB=5,BC=4,点D为边AC上的动点,作菱形DEFG,使点E、F在边AB上,点G在边BC上.若这样的菱形能作出两个,则AD的取值范围是( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com