
【题目】运动员将足球沿与地面成一定角度的方向踢出,足球飞行的路线是一条抛物线,不考虑空气阻力,足球距离地面的高度h(单位:m)与足球被踢出后经过的时间t(单位:s)之间的关系如下表:
t | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | … |
h | 0 | 8 | 14 | 18 | 20 | 20 | 18 | 14 | … |
下列结论:①足球距离地面的最大高度为20m;②足球飞行路线的对称轴是直线t=![]() ;③足球被踢出9.5s时落地:④足球被踢出7.5s时,距离地面的高度是11.25m,其中不正确结论的个数是( )
;③足球被踢出9.5s时落地:④足球被踢出7.5s时,距离地面的高度是11.25m,其中不正确结论的个数是( )
A. 1 B. 2 C. 3 D. 4
【答案】B
【解析】
根据表格中的数据和题意设出抛物线解析式h=at2+bt+c,再将(0,0)、(1,8)、(2,14)代入,可以求得相应的函数解析式,从而可以判断各个小题中的结论是否成立,从而可以解答本题.
解:设该抛物线的解析式为h=at2+bt+c,(0,0)、(1,8)、(2,14)代入,

解得,
所以可以得到h=-t2+9t=-(t-4.5)2+20.25
(1)当t=4.5时,足球距离地面的最大高度为20.25m,故①错误,
(2)抛物线的对称轴t=4.5,故②正确,
(3)当h=0,时t=0或t=9,足球被踢出9s时落地,故③错误,
(4)t=7.5时,h=11.25,故④正确.
∴正确的有②④,不正确的有①③,不正确的个数为2
故选:B.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
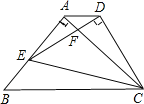
【题目】 如图,△ABC为等腰直角三角形,∠BAC=90°,BC=1,E为直角边AB上任意一点,以线段CE为斜边作等腰Rt△CDE,连接AD,下列说法:①AC⊥ED;②∠BCE=∠ACD;③△AED∽△ECB;④AD∥BC;⑤四边形ABCD面积的最大值为![]() ,其中正确的是______________.
,其中正确的是______________.
查看答案和解析>>
科目:初中数学 来源: 题型:
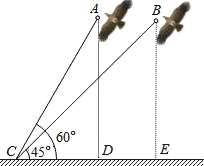
【题目】在一个阳光明媚,微风习习的周末,小明和小强一起到聂耳文化广场放风筝,放了一会儿,两个人争吵起来:小明说:“我的风筝飞得比你的高”.小强说:“我的风筝引线比你的长,我的风筝飞得更高”.谁的风筝飞得更高呢?于是他们将两个风筝引线的一段都固定在地面上的C处(如图),现已知小明的风筝引线(线段AC)长30米,小强的风筝引线(线段BC)长36米,在C处测得风筝A的仰角为60°,风筝B的仰角为45°,请通过计算说明谁的风筝飞得更高?(结果精确到0.1米,参考数据:![]() ≈1.41,
≈1.41,![]() ≈1.73)
≈1.73)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠C=90°,Rt△BAP中,∠BAP=90°,已知∠CBO=∠ABP,BP交AC于点O,E为AC上一点,且AE=OC.
(1)求证:AP=AO;
(2)求证:PE⊥AO;
(3)当AE=![]() AC,AB=10时,求线段BO的长度.
AC,AB=10时,求线段BO的长度.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠C=90°,点A、B在∠C的两边上,CA=30,CB=20,连接AB.点P从点B出发,以每秒4个单位长度的速度沿BC的方向运动,到点C停止.当点P与B、C两点不重合时,作PD⊥BC交AB于点D,作DE⊥AC于点E.F为射线CB上一点,使得∠CEF=∠ABC.设点P运动的时间为x秒.
(1)用含有x的代数式表示CE的长.
(2)求点F与点B重合时x的值.
(3)当点F在线段CB上时,设四边形DECP与四边形DEFB重叠部分图形的面积为y(平方单位).求y与x之间的函数关系式.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠B=90°,AB=12,BC=24,动点P从点A开始沿边AB向终点B以每秒2个单位长度的速度移动,动点Q从点B开始沿边BC以每秒4个单位长度的速度向终点C移动,如果点P、Q分别从点A、B同时出发,那么△PBQ的面积S随出发时间t(s)如何变化?写出函数关系式及t的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
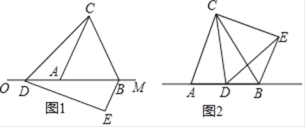
【题目】已知△ABC是边长为4的等边三角形,边AB在射线OM上,且OA=6,点D是射线OM上的动点,当点D不与点A重合时,将△ACD绕点C逆时针方向旋转60°得到△BCE,连接DE.
(1)如图1,求证:△CDE是等边三角形.
(2)设OD=t,
①当6<t<10时,△BDE的周长是否存在最小值?若存在,求出△BDE周长的最小值;若不存在,请说明理由.
②求t为何值时,△DEB是直角三角形(直接写出结果即可).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,Rt△ABC中,∠ABC=90°,以AB为直径作⊙O,点D为⊙O上一点,且CD=CB、连接DO并延长交CB的延长线于点E.
(1)判断直线CD与⊙O的位置关系,并说明理由;
(2)若BE=4,DE=8,求AC的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,∠ACB=90°,sinA=![]() ,BC=8,点D是AB的中点,过点B作CD的垂线,垂足为点E.
,BC=8,点D是AB的中点,过点B作CD的垂线,垂足为点E.
(1)求线段CD的长;
(2)求cos∠ABE的值。

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com